
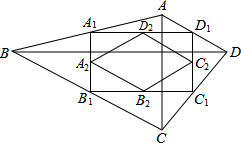
 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )| A. | ①②③ | B. | ②③④ | C. | ①② | D. | ②③ |
分析 首先根据题意,找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律,然后对以下选项作出分析与判断:
①根据矩形的判定与性质作出判断;
②根据菱形的判定与性质作出判断;
③由四边形的周长公式:周长=边长之和,来计算四边形A5B5C5D5的周长;
④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积.
解答 解:①连接A1C1,B1D1.
∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,∴四边形A1B1C1D1是矩形,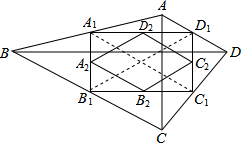
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
故本选项错误;
②由①知,四边形A2B2C2D2是菱形;
∴根据中位线定理知,四边形A4B4C4D4是菱形;
故本选项正确;
③根据中位线的性质易知,A5B5=$\frac{1}{2}$A3B3=$\frac{1}{2}$A1B1=$\frac{1}{2}$AC,B5C5=$\frac{1}{2}$B3C3=$\frac{1}{2}$B1C1=$\frac{1}{2}$BD,
∴四边形A5B5C5D5的周长是2×$\frac{1}{8}$(a+b)=$\frac{a+b}{4}$,
故本选项正确;
④∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是$\frac{ab}{{2}^{n+1}}$,
故本选项正确;
综上所述,②③④正确.
故选:B.
点评 本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半).解答此题时,需理清菱形、矩形与平行四边形的关系.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a∥b,b∥c,则a∥c | B. | 若a⊥b,b⊥c,则a⊥c | C. | 若a∥b,b⊥c,则a∥c | D. | 若a∥b,b∥c,则a⊥c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是( )
如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是( )| A. | (50,51) | B. | (49,50) | C. | (51,50) | D. | (50,49) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40(1-x)2=40-28 | B. | 40(1-2x)=28 | C. | 40(1-x)2=28 | D. | 40(1-x2)=28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5% | B. | 10% | C. | 19% | D. | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.07,$\frac{2}{3}$,$\sqrt{7}$ | B. | 0.7,$\sqrt{5}$,$\sqrt{4}$ | C. | $\sqrt{2}$,$\sqrt{6}$,π | D. | 3.14,$\sqrt{3}$,$\frac{22}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com