
如图1,已知菱形ABCD的边长为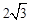 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- 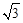 ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t< 3 )
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)
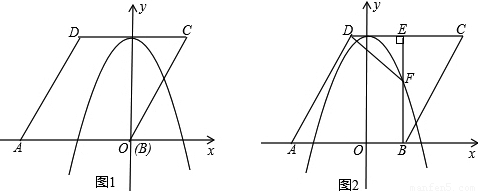
(1)y=-x2+3(2)①存在,t=1②
【解析】解:(1)由题意得AB的中点坐标为(-3 ,0),CD的中点坐标为(0,3),
分别代入y=ax2+b,得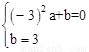 ,解得,
,解得,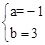 。
。
∴这条抛物线的函数解析式为y=-x2+3。
(2)①存在。如图2所示,在Rt△BCE中,∠BEC=90°,BE=3,BC= ,
,
∴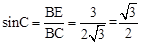 。∴∠C=60°,∠CBE=30°。∴EC=
。∴∠C=60°,∠CBE=30°。∴EC= BC=
BC=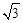 ,DE=
,DE=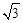 。
。
又∵AD∥BC,∴∠ADC+∠C=180°。∴∠ADC=180°-60°=120°
要使△ADF与△DEF相似,则△ADF中必有一个角为直角。
(I)若∠ADF=90°,∠EDF=120°-90°=30°。
在Rt△DEF中,DE=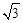 ,得EF=1,DF=2。
,得EF=1,DF=2。
又∵E(t,3),F(t,-t2+3),∴EF=3-(-t2+3)=t2。∴t2=1。
∵t>0,∴t=1 。
此时 ,∴
,∴ 。
。
又∵∠ADF=∠DEF,∴△ADF∽△DEF。
(II)若∠DFA=90°,可证得△DEF∽△FBA,则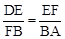 。
。
设EF=m,则FB=3-m。
∴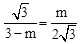 ,即m2-3m+6=0,此方程无实数根。∴此时t不存在。
,即m2-3m+6=0,此方程无实数根。∴此时t不存在。
(III)由题意得,∠DAF<∠DAB=60°,∴∠DAF≠90°,此时t不存在。
综上所述,存在t=1,使△ADF与△DEF相似。
②
(1)根据已知条件求出AB和CD的中点坐标,然后利用待定系数法求该二次函数的解析式。
(2)①如图2所示,△ADF与△DEF相似,包括三种情况,需要分类讨论:
(I)若∠ADF=90°时,△ADF∽△DEF,求此时t的值。
(II)若∠ADF=90°时,△DEF∽△FBA,利用相似三角形的对应边成比例可以求得相应的t的值。
(III)∠DAF≠90°,此时t不存在。
 ②画出旋转后的图形,认真分析满足题意要求时,需要具备什么样的限制条件,然后根据限制条件列出不等式,求出t的取值范围:
②画出旋转后的图形,认真分析满足题意要求时,需要具备什么样的限制条件,然后根据限制条件列出不等式,求出t的取值范围:
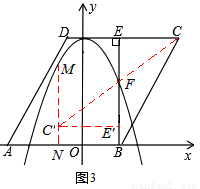
如图3所示,依题意作出旋转后的三角形△FE′C′,过C′作MN⊥x轴,分别交抛物线、x轴于点M、点N。
观察图形可知,欲使△FE′C′落在指定区域内,必须满足:EE′≤BE且MN≥C′N。
∵F(t,3-t2),∴EF=3-(3-t2)=t2。∴EE′=2EF=2t2。
由EE′≤BE,得2t2≤3,解得 。
。
又∵C′E′=CE=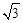 ,∴C′点的横坐标为t-
,∴C′点的横坐标为t-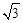 。∴MN=3-(t-
。∴MN=3-(t-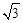 )2,
)2,
又C′N=BE′=BE-EE′=3-2t2,
∴由MN≥C′N,得3-(t-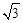 )2≥3-2t2,即t2+2
)2≥3-2t2,即t2+2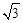 t-3≥0。
t-3≥0。
求出t2+2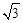 t-3=0,得
t-3=0,得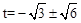 ,∴t2+2
,∴t2+2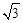 t-3≥0即
t-3≥0即 。
。
∵ ,∴
,∴ ,解得t≥
,解得t≥ 。
。
∴t的取值范围为:


科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 2 |
| a |
| s |

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,已知菱形ABCD的边长为![]() ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- ![]() ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t< 3 )
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”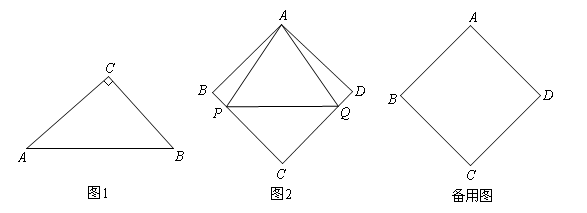
(1)请用直尺与圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°, ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a, ∠ABC=2β,点P,Q从点A同时出发,以相同的速度分别沿折线AB-BC和AD-DC向终点C运动,记点P所经过的路程为s
①当β=45°时,若△APQ是“好玩三角形”,试求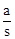 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”?请直接写出tanβ的取值范围。
(4)本小题为选做题
依据(3)中的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是“好玩三角形”的个数关系”的真命题(“好玩三角形”的个数限定不能为1)。
查看答案和解析>>
科目:初中数学 来源:2013年四川省眉山市中考适应性考试数学试卷(解析版) 题型:解答题
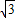 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-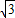 ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.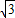 )
)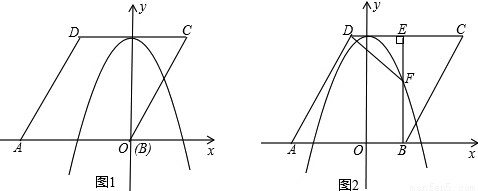
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com