
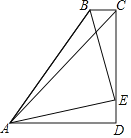
【题目】如图,四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°,若CD=4,则DE长为_____.
【答案】![]()
【解析】
过C点作CF∥AB交AD于点F,设BC=AF=a,根据平行四边形和等腰直角三角形的性质构造平行四边形,根据勾股定理,求出梯形上底长,再根据梯形面积等于三个三角形面积和求解即可.
解:如图:
过C点作CF∥AB交AD于点F,∵AD∥BC,
∴四边形ABCF是平行四边形,∴CF=AB,BC=AF,
设BC=AF=a,
∵AD∥BC,∠BCD=90°,∠DAC=45°,
∴∠DAC=∠DCA=45°,
∴AD=CD=4,
∴DF=AD﹣AF=4﹣a,
∵AB=BC+AD,
∴CF=AB=a+4.
在Rt△CDF中,根据勾股定理,得
(a+4)2=(4﹣a)2+42,解得a=1,
∴BC=1,AB=5.
作EH⊥AB于点H,∵∠EAB=45°,
∴∠AEH=45°,
∴AH=EH=![]() AE.
AE.
设DE=x,则CE=4﹣x,
在Rt△ADE中,AE=![]() ,S△ADE=
,S△ADE=![]() ADDE=2x.
ADDE=2x.
在Rt△BCE中,S△BCE=![]() BCCE=
BCCE=![]() (4﹣x).
(4﹣x).
在Rt△ABE中,S△ABE=![]() ABEH=
ABEH=![]() .
.
S梯形ABCD=![]() CD(BC+AD)=10.
CD(BC+AD)=10.
S梯形ABCD=S△ADE+S△BCE+S△ABE,
即10=2x+![]() (4﹣x)+
(4﹣x)+![]() .
.
整理得:7x2+192x﹣112=0,
解得:x=![]() 或x=﹣28(舍去).
或x=﹣28(舍去).
所以DE的长为![]() ./p>
./p>
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=4π,BC=3π,半径是2的⊙O从与AC相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AC相切于点D的位置,则⊙O自转了( )

A.2周B.3周C.4周D.5周
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°
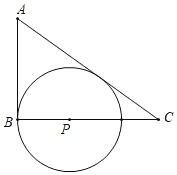
(1)在BC边上找一点P,作⊙P与AC,AB边都相切,与AC的切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=4,AC=6,求第(1)题中所作圆的半径;
(3)连接BQ,第(2)题中的条件不变,求cos∠CBQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-4n+4经过点P(2,4),与x轴交于A、B两点,过点P作直线l∥x轴,点C为第二象限内直线l上方,抛物线上一个动点,其横坐标为m。
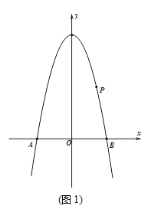
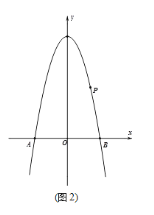

(1)如图(1),若AB=6, 求抛物线解析式
(2)如图(2),在(1)的条件下,设点C的横坐标为t,ACP的面积S,求S与t之间的函数关系式.
(3)如图(3),连接OP,过点C作EC∥OP交抛物线于点E,直线PE、CP分别交x轴于点G、H,当PG=PH时,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以数轴的原点O为圆心,以3为半径的圆,∠AOB=45°,点P在数轴上运动.若过点P与OA平行的直线与⊙O有公共点,设点P在数轴上表示的数为x.则x的取值范围是( )

A.0≤x≤3![]() B.x>3
B.x>3![]() C.﹣3≤x≤3D.﹣3
C.﹣3≤x≤3D.﹣3![]() ≤x≤3
≤x≤3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )

A.17B.18C.19D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
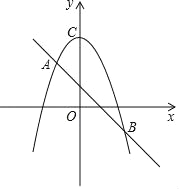
【题目】如图,一次函数y=kx+b的图象与二次函数y=﹣x2+c的图象相交于A(﹣1,2),B(2,n)两点.
(1)求一次函数和二次函数的解析式;
(2)根据图象直接写出使二次函数的值大于一次函数的值的x的取值范围;
(3)设二次函数y=﹣x2+c的图象与y轴相交于点C,连接AC,BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
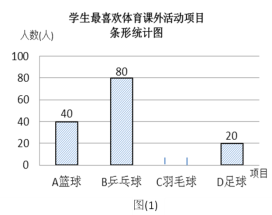
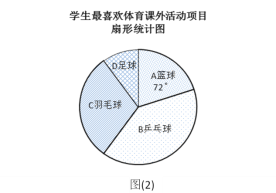
【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请你将条形统计图(1)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
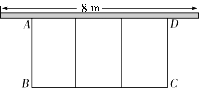
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com