
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图,对于下列说法:①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中正确的是( )
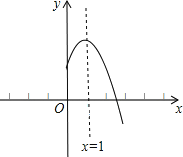
A.①②B.①③C.①②③D.①②④
【答案】C
【解析】
首先根据二次函数图象开口方向可得a<0,根据图象与y轴交点可得c>0,再根据二次函数的对称轴x=﹣![]() ,结合a的取值可判定出b>0,根据a、b、c的正负即可判断出①的正误;把x=﹣1代入函数关系式y=ax2+bx+c中得y=a﹣b+c,再结合图象判断出②的正误;把b=﹣2a代入a﹣b+c中即可判断出③的正误;利用图象可以直接看出④的正误.
,结合a的取值可判定出b>0,根据a、b、c的正负即可判断出①的正误;把x=﹣1代入函数关系式y=ax2+bx+c中得y=a﹣b+c,再结合图象判断出②的正误;把b=﹣2a代入a﹣b+c中即可判断出③的正误;利用图象可以直接看出④的正误.
解:根据图象可得:a<0,c>0,
对称轴:x=﹣![]() =1,
=1,
b=﹣2a,
∵a<0,
∴b>0,
∴abc<0,
故①正确;
把x=﹣1代入函数关系式y=ax2+bx+c中得:y=a﹣b+c,
由图象可以看出当x=﹣1时,y<0,
∴a﹣b+c<0,
故②正确;
∵b=﹣2a,
∴a﹣(﹣2a)+c<0,
即:3a+c<0,故③正确;
由图形可以直接看出④错误.
正确的有①②③.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
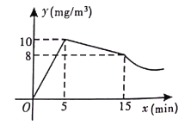
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
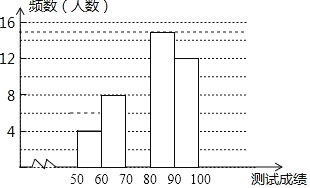
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD对角线AC上的一个动点(点E可以与点A和点C重合),连接BE.已知AB=3cm,BC=4cm.设A、E两点间的距离为xcm,BE的长度为ycm.

某同学根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是该同学的探究过程,请补充完整:
(1)通过取点、画图、测量及分析,得到了x与y的几组值,如下表:

说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当BE=2AE时,AE的长度约为 cm.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,以此类推,为了投资少而获利大,每个遮阳伞每天应提高_______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月,以“寻根国学,传承文明”为主题的某市第三届“国学少年强﹣﹣﹣国学知识挑战赛”总决赛拉开帷幕.小明晋级了总决赛,比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用A1,A2,A3,A4表示);
第二环节:成语听写、诗词对句、经典诵读(分别用B1,B2,B3表示).
(1)计算小明在第一环节抽取的题目是国学常识的概率;
(2)用树状图或列表法,计算小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点A逆时针旋转,使点D落在⊙O上,若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为( )

A.2πcmB.![]() cmC.πcmD.
cmC.πcmD.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点M是y轴正半轴上的任意一点,过点M作PQ∥x轴,分别交函数y=![]() (y>0)和y=
(y>0)和y=![]() (y>0)的图象于点P和Q,连接OP和OQ,则下列结论正确是( )
(y>0)的图象于点P和Q,连接OP和OQ,则下列结论正确是( )
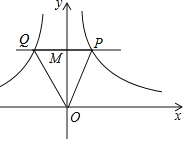
A.∠POQ不可能等于90°
B.![]()
C.这两个函数的图象一定关于y轴对称
D.△POQ的面积是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.

(1)求证:∠BAP=∠CAP;
(2)判断直线PC与⊙O的位置关系,并说明理由;
(3)若AB=5![]() ,BC=10,求PC的长.
,BC=10,求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com