
【题目】下列说法中,正确的有( ) ①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
A.3个
B.2个
C.1个
D.0个
科目:初中数学 来源: 题型:
【题目】有下列说法:①电线杆可看做射线,②探照灯光线可看做射线,③A地到B地的高速公路可看做一条直线.其中正确的有( )
A. 0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十九大报告中提出“广泛开展全民健身活动,加快推进体育强国建设”.为了响应号召,提升学生训练兴趣,某中学自编“功夫扇”课间操.若设最外侧两根大扇骨形成的角为∠COD,当“功夫扇”完全展开时∠COD=160°.在扇子舞动过程中,扇钉O始终在水平线AB上.
小华是个爱思考的孩子,不但将以上实际问题抽象为数学问题,而且还在抽象出的图中画出了∠BOC 的平分线OE,以便继续探究.
(1)当扇子完全展开且一侧扇骨OD呈水平状态时,如图1所示.请在抽象出的图2中画出∠BOC 的平分线OE,此时∠DOE的度数为 ;

(2)“功夫扇”课间操有一个动作是把扇子由图1旋转到图3所示位置,即将图2中的∠COD绕点O旋转至图4所示位置,其他条件不变,小华尝试用如下两种方案探究了∠AOC和∠DOE度数之间的关系.

方案一:设∠BOE的度数为x.
可得出![]() ,则
,则![]() .
.
![]() ,则
,则![]() .
.
进而可得∠AOC和∠DOE度数之间的关系.
方案二:如图5,过点O作∠AOC的平分线OF.

易得![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() .
.
进而可得∠AOC和∠DOE度数之间的关系.
参考小华的思路可得∠AOC和∠DOE度数之间的关系为 ;
(3)继续将扇子旋转至图6所示位置,即将∠COD绕点O旋转至如图7所示的位置,其他条件不变,请问(2)中结论是否依然成立?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列第(1)题中的计算方法,再计算第(2)题中式子的值.
(1)﹣![]() +(﹣9
+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
解:原式=[(﹣5)+(﹣![]() )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣![]() )]+[(+17)+(+
)]+[(+17)+(+![]() )]+[(﹣3)+(﹣
)]+[(﹣3)+(﹣![]() )]
)]
=[(﹣5)+(﹣9)+(+17)+(﹣3)]+[(﹣![]() )+(﹣
)+(﹣![]() )+(+
)+(+![]() )+(﹣
)+(﹣![]() )]
)]
=0+(﹣1![]() )
)
=﹣1![]()
上面这种方法叫拆项法.仿照上述方法计算:
(2)(﹣2008![]() )+(﹣2007
)+(﹣2007![]() )+4017
)+4017![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机构对2016年微信用户的职业颁布进行了随机抽样调查(职业说明:A:党政机关、军队,B:事业单位,C:企业,D:自由职业及人体户,E:学生,F:其他),图1和图2是根据调查数据绘制而成的不完整的统计图.请根据图中提供的信息,解答下列问题:
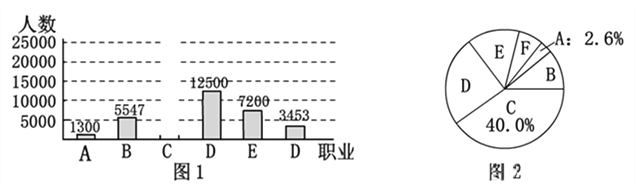
(1)该机构共抽查微信用户___________人;
(2)在图.1中,补全条形统计图;
(3)在图2中,“D”用户所对应扇形的圆心角度数为___________度;
(4)2016年微信用户约有7.5亿人,估计“E”用户大约有________亿人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com