
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
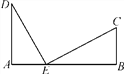
【答案】E站应建在离A站10千米处.
【解析】试题分析:根据C、D两村到E站的距离相等,可得DE=CE,在Rt△AED和Rt△EBC中,根据勾股定理可得AE2+AD2=BE2+BC2,设AE=x,则BE=25﹣x,列出方程,解方程求得x的值,即可得收购站E离A点的距离.
试题解析:
∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB﹣AE=(25﹣x),
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,则AD是 ∠BAC的平分线吗?若是说明理由.(在下面的括号内填注依据)
解:是,理由如下:

∵AD⊥BC,EG⊥BC ( 已知 ),
∴∠4=∠5=90( 垂直的定义),
∴AD‖_____( );
∴∠1=∠E ( ),
∠2=______(两直线平行,内错角相等);
∵∠E=∠3(已知),
∴∠_____=∠____(等量代换);
∴AD平分∠BAC( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com