
 如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.
如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.分析 (1)根据题意画出线段AC即可;
(2)求出AC长求出BC,根据线段中点求出CD即可;
(3)根据(2)得出方程,求出方程的解即可.
解答 解:(1)如图,线段AC,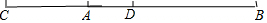 ;
;
(2)∵AB=a,AC=$\frac{1}{2}$AB,
∴AC=$\frac{1}{2}$a,
∴BC=AC+AB=$\frac{3}{2}$a,
∵点D为线段BC的中点,
∴CD=$\frac{1}{2}$BC=$\frac{3}{4}$a;
(3)∵AD=6,AD=CD-AC,
由(2)可知:AC=$\frac{1}{2}$a,CD=$\frac{3}{4}$a,
∴$\frac{3}{4}$a-$\frac{1}{2}$a=6,
解得:a=24.
点评 本题考查了线段的中点和求两点之间的距离等知识点,能求出各个线段的长是解此题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )| A. | 12$\sqrt{3}$ | B. | 18 | C. | 6$\sqrt{3}$+6 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$a≥-7 | B. | $\frac{1}{2}$a≤-7 | C. | $\frac{1}{2}$a>-7 | D. | $\frac{1}{2}a<-7$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
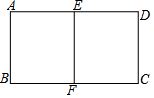 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )| A. | 2 | B. | $\frac{5}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com