
【题目】某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)如果果园既要让橙子的总产量达到60375个,又要确保每一棵橙子树接受到的阳光照射尽量少受影响,那么应该多种多少棵橙子树?
(2)增种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?
科目:初中数学 来源: 题型:
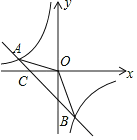
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
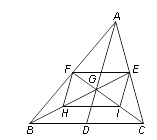
【题目】如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1)求证:四边形EFHI是平行四边形;
(2)①当AD与BC满足条件 时,四边形EFHI是矩形;
②当AD与BC满足条件 时,四边形EFHI是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:不在同一直线上的三点A,B,C
求作:⊙O,使它经过点A,B,C
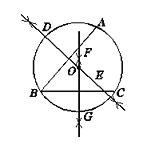
作法:如图,
(1)连接AB ,作线段AB的垂直平分线DE;
(2)连接BC ,作线段BC的垂直平分线FG,交DE于点O;
(3)以O为圆心,OB 长为半径作⊙O.
⊙O就是所求作的圆.
根据以上作图过程及所作图形,下列结论中正确的是( )
A.连接AC, 则点O是△ABC的内心B.![]()
C.连接OA,OC,则OA, OC不是⊙![]() 的半径D.若连接AC, 则点O在线段AC的垂直平分线上
的半径D.若连接AC, 则点O在线段AC的垂直平分线上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知P(
中,已知P(![]() ,
,![]() ),R(
),R(![]() ,
,![]() )两点,且
)两点,且![]() ,
,![]() ,若过点P作
,若过点P作![]() 轴的平行线,过点R作
轴的平行线,过点R作![]() 轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作
轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作![]() 轴的平行线,过点P作
轴的平行线,过点P作![]() 轴的平行线,两平行线交于一点
轴的平行线,两平行线交于一点![]() ,连接PR,则称△RP
,连接PR,则称△RP![]() 为点R,P,
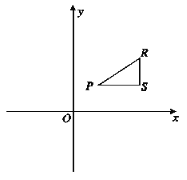
为点R,P,![]() 的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
(1)已知点A(0,4),点B(3,0),若△ABC是点A,B,C的“坐标轴三角形”,则点C的坐标为 ;
(2)已知点D(2,1),点E(e,4),若点D,E,F的“坐标轴三角形”的面积为3,求e的值.
(3)若![]() 的半径为
的半径为![]() ,点M(
,点M(![]() ,4),若在
,4),若在![]() 上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求
上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是测量一物体体积的过程:
步骤一:将180 mL的水装进一个容量为300 mL的杯子中;
步骤二:将三个相同的玻璃球放入水中,结果水没有满;
步骤三:再将一个同样的玻璃球放入水中,结果水满溢出.

根据以上过程,推测一个玻璃球的体积在下列哪一范围内?(1 mL=1 cm3)( ).
A. 10 cm3以上,20 cm3以下 B. 20 cm3以上,30 cm3以下
C. 30 cm3以上,40 cm3以下 D. 40 cm3以上,50 cm3以下
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com