
 矩形ABCD的边BC在直线l上,AB=2,BC=4,P是AD边上一动点且不与点D重合,连结CP,过点P作∠APE=∠CPD,交直线l于点E,若PD的长为x,△PEC与矩形ABCD重合部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
矩形ABCD的边BC在直线l上,AB=2,BC=4,P是AD边上一动点且不与点D重合,连结CP,过点P作∠APE=∠CPD,交直线l于点E,若PD的长为x,△PEC与矩形ABCD重合部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. |  | B. |  | C. | 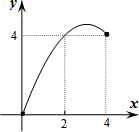 | D. | 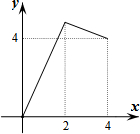 |
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
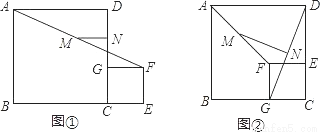
(1)线段MN和GD的数量关系是 ,位置关系是 ;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
如图,在?ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
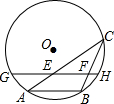 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为6,则GE+FH的最大值为9.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为6,则GE+FH的最大值为9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=-(b-a)2 | B. | $\frac{1}{{x}^{3}}$=x-3 | C. | $\frac{{a}^{2}+1}{a+1}$=a+1 | D. | x6÷x2=x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
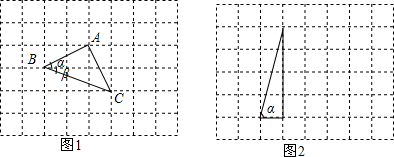
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间的距离是两点间的线段 | |
| B. | 同一平面内,过一点有且只有一条直线与已知直线平行 | |
| C. | 与同一条直线垂直的两条直线也垂直 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com