
����Ŀ����ͼ��Rt��OAB��ͼ��ʾ������ƽ��ֱ������ϵ�У�ֱ�DZ�OA��x���غϣ���OAB=90�㣬OA=4��AB=2����Rt��OAB�Ƶ�O��ʱ����ת90�㣬��B��ת����C��λ�ã�һ�����������þ�����O��C��A���㣮
��1����������ߵĽ���ʽ��
��2����x���Ϸ�������������һ����P������P��x���ƽ���߽��������ڵ�M���ֱ����P����M��x��Ĵ��ߣ���x����E��F���㣬�ʣ��ı���PEFM���ܳ��Ƿ������ֵ������У��������ֵ����д�������̣����û�У���˵�����ɣ�
��3�����x������һ����H�������������Ƿ���ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ������ڣ����N������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ΪOA=4��AB=2���ѡ�AOB�Ƶ�O��ʱ����ת90�㣬
����ȷ����C������Ϊ��2��4������ͼ��֪��A������Ϊ��4��0����
����Ϊ�����߾���ԭ�㣬����y=ax2+bx�ѣ�2��4������4��0�����룬
�� ![]() �����
����� ![]()
���������ߵĽ���ʽΪy=��x2+4x��
��2��
�⣺�ı���PEFM���ܳ������ֵ���������£�
�����⣬��ͼ��ʾ�����P������ΪP��a����a2+4a�����������ߵĶԳ���֪OE=AF��
��EF=PM=4��2a��PE=MF=��a2+4a��
�����PEFM���ܳ�L=2[4��2a+����a2+4a��]=��2��a��1��2+10��
�൱a=1ʱ������PEFM���ܳ������ֵ��Lmax=10��
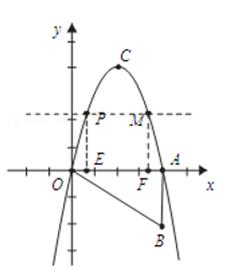
��3��
�⣺���������ϴ��ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ��������£�
��y=��x2+4x=����x��2��2+4��֪�������꣨2��4����
��֪��C�������Ƕ������֪꣬��C�㵽x��ľ���Ϊ4����λ���ȣ�
����C��x���ƽ���ߣ���x��û���������㣬��y=��4��x���ƽ���ߣ������������������㣬
����������Ϊ�����N�����������Щ�x2+4x=��4 ���x1=2+ ![]() ��x2=2��
��x2=2�� ![]()
��N������ΪN1��2+ ![]() ����4����N2��2��
����4����N2��2�� ![]() ����4����
����4����

����������1��������ת�����ʿ����C�������A�����꣬����Ϊ�����߾���ԭ�㣬����y=ax2+bx�ѣ�2��4������4��0�����룬���a��b��ֵ��������������ߵĽ���ʽ����2���ı���PEFM���ܳ������ֵ�����P������ΪP��a����a2+4a�����������ߵĶԳ���֪OE=AF������EF=PM=4��2a��PE=MF=��a2+4a�������PEFM���ܳ�L=2[4��2a+����a2+4a��]=��2��a��1��2+10�����ú��������ʼ�������ı���PEFM���ܳ������ֵ����3�����������ϴ��ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ��ɣ�1������������ߵĶ������꣬����C��x���ƽ���ߣ���x��û���������㣬��y=��4��x���ƽ���ߣ������������������㣬����������Ϊ�����N�����������Щ�x2+4x=��4���ⷽ�̼�������������꣮
�����㾫�������ն��κ����������ǽ����ĸ�������Ҫ֪�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y��2x��5��x���y��ֱ��ڵ�A�͵�B����C��1��n����ֱ��AB�ϣ���D��y��ĸ������ϣ���CD=![]() ��
��
��1�����C����D������.
��2����PΪy���ϵĵ㣬����PCDΪ����������ʱ�����P������.
��3������MΪx����һ���㣨��M�����O�غϣ���NΪֱ��y��2x��5��һ���㣬�Ƿ���ڵ�M��N��ʹ�á�AMN���AOBȫ�ȣ������ڣ������N�����ꣻ�������ڣ���˵�����ɣ�


ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(2,0)��B(2,4)�����壺��ƽ���ڵ�P����ֱ��AB�ĶԳƵ�Q��ͼ��M�ڻ�ͼ�εı߽��ϣ���Ƶ�P��ͼ��M����ֱ��AB�������Ƶ���.
��1����֪C(5,0)��D(5,3)
�ٵ�M1(0,3)��M2(-0. 5,2)��M3(-2,1)��������ACD����ֱ��AB�������Ƶ�������________��
����ֱ��y=2x+m�ϴ�����ACD����ֱ��AB�������Ƶ�������m��ȡֵ��Χ��
��2����֪��E(1,0)��F(5,0)�� ![]() ����P(x��y)��ֱ��y=x+1�ϣ��ҵ�P����EFG�ķ��Ƶ㣬���P�������ȡֵ��Χ.
����P(x��y)��ֱ��y=x+1�ϣ��ҵ�P����EFG�ķ��Ƶ㣬���P�������ȡֵ��Χ.
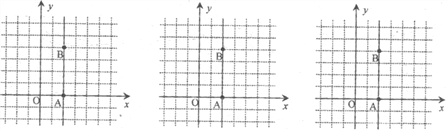
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬ADƽ�֡�BAC��DE��AB��E�������н��ۣ���DE��CD����ADƽ�֡�CDE���ۡ�BAC����BDE����BE+AC��AB��������ȷ���ǣ� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪С��ijɼ����±���
�Ļ��ɼ� | �ۺ��� �ʳɼ� | �ܳɼ� | |||
����1 | ����2 | ����3 | |||
�� | 560�� | 580�� | 630�� | 12 | |
��1��С����������Ļ����Գɼ���ƽ������_____�֣�
��2���ã�1���е�ƽ���ּ����ۺ����ʳɼ�����С����ܳɼ�����ͬ���ķ��������С�����ڰ༶ȫ��ͬѧ���ܳɼ������Ƴ�����ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ����ôС�����ڰ༶����_____��ͬѧ��
��3��ѧУ�������ܳɼ��ɸߵ��ͱ���С�����ڰ༶ǰ15��ͬѧ�������ѧϰ������С���ܱ�������˵�����ɣ�
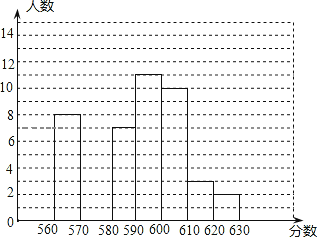
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ���ı���OABC��,��֪��A��C���������ΪA (![]() ,
,![]() ),C (2
),C (2![]() ,0).
,0).
(1)���B������.
(2)��ƽ���ı���OABC����ƽ��![]() ����λ����,�������ı���A��B��C��O���ĸ����������.
����λ����,�������ı���A��B��C��O���ĸ����������.
(3)��ƽ���ı���OABC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ����Ⱥ�Ľ����뷢չ����A��B�����м��½�һ���Ǽ���·�����ɺ���·������������ڵ�120km������114km���Ǽ���·�����ƽ��ʱ��Ҫ�����е�ƽ��ʱ�ٿ�110km������ʱ���������ʱ���![]() ���ɺ�ijǼ���·��A��B���ص�����ʱ�䣮
���ɺ�ijǼ���·��A��B���ص�����ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C���ҵ�B���C������ֱ�ΪB��3��0����C��0��3������M�������ߵĶ��㣮
��1������κ����Ĺ�ϵʽ��
��2����PΪ�߶�MB��һ�����㣬����P��PD��x���ڵ�D����OD=m����PCD�����ΪS�����ж�S�����ֵ����Сֵ����˵�����ɣ�
��3����MB���Ƿ���ڵ�P��ʹ��PCDΪֱ�������Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC��![]() �ϵĸߣ�BEƽ�֡ϡ�ABC��AD�ڵ�E������C=60�㣬��BED=70�㣮 ���ABC�͡�BAC�Ķ�����
�ϵĸߣ�BEƽ�֡ϡ�ABC��AD�ڵ�E������C=60�㣬��BED=70�㣮 ���ABC�͡�BAC�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com