
【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=﹣1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.其中正确的结论有( )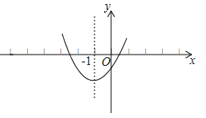
A.2个
B.3个
C.4个
D.5个
【答案】B
【解析】解:(1)抛物线与x轴有2个交点,则b2﹣4ac>0,则b2>4ac,故(1)正确;
(2)抛物线开口方向向上,则a>0.
抛物线与y轴交于负半轴,则c<0.
对称轴在y轴的左侧,a、b同号,即b>0.
所以abc<0.故(2)错误;
(3)对称轴x=﹣![]() =﹣1,则b﹣2a=0,故(3)错误;
=﹣1,则b﹣2a=0,故(3)错误;
(4)如图,当x=1时,y>0,即a+b+c>0,故(4)正确;
(5)如图,当x=﹣时,y<0,即a﹣b+c<0.故(5)正确;
综上所述,正确的个数是3个.
故选:B.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
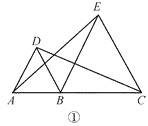
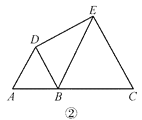
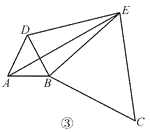
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
(2)如图②,若 AB=1,BC=2,求 DE 的长;
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
(1)求证:ABAF=CBCD;
(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP的面积为ycm2 .
①求y关于x的函数关系式.
②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.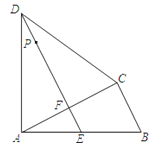
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正确的结论是( )
.其中正确的结论是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
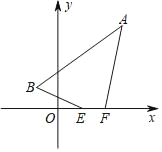
【题目】已知点A(3,4),点B(﹣1,1),在x轴上有两动点E、F,且EF=1,线段EF在x轴上平移,当四边形ABEF的周长取得最小值时,点E的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.
(1)求出该品牌应急灯、手电筒的定价分别是多少元?
(2)经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com