
【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往![]() 县10辆,需要调往
县10辆,需要调往![]() 县8辆,已知从甲仓库调运一辆农用车到
县8辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为40元和80元;从乙仓库调运一辆农用车到
县的运费分别为40元和80元;从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为30元和50元.
县的运费分别为30元和50元.
(1)设乙仓库调往![]() 县农用车
县农用车![]() 辆,求总运费
辆,求总运费![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若要求总运费不超过900元,问共有几种调运方案?试列举出来.
(3)求出总运费最低的调运方案,最低运费是多少元?
【答案】(1)![]()
![]() ;(2)3种;方案一:甲调往
;(2)3种;方案一:甲调往![]() :10辆;乙往
:10辆;乙往![]() :0辆;甲调往
:0辆;甲调往![]() :2辆;乙调往
:2辆;乙调往![]() :6辆; 方案二:甲调往
:6辆; 方案二:甲调往![]() :9辆;乙往
:9辆;乙往![]() :1辆;甲调往
:1辆;甲调往![]() :3辆;乙调往
:3辆;乙调往![]() :5辆;方案三:甲调往
:5辆;方案三:甲调往![]() :8辆;乙往
:8辆;乙往![]() :2辆;甲调往
:2辆;甲调往![]() :4辆;乙调往
:4辆;乙调往![]() :4辆;(3)方案一的总运费最少为860元.
:4辆;(3)方案一的总运费最少为860元.
【解析】
(1)若乙仓库调往A县农用车x辆,那么乙仓库调往B县农用车、甲给A县调农用车、以及甲县给B县调车数量都可表示出来,然后依据各自运费,把总运费表示即可;
(2)若要求总运费不超过900元,则可根据(1)列不等式确定x的取值,从而求解;
(3)在(2)的基础上,结合一次函数的性质求出最低运费即可.
解:(1)乙仓库调往![]() 县农用车
县农用车![]() 辆,则调往
辆,则调往![]() 县农用车
县农用车![]() 辆.
辆.![]()
![]() 县需10辆车,故甲给
县需10辆车,故甲给![]() 县调
县调![]() 辆,给
辆,给![]() 县调车
县调车![]() 辆
辆
∴![]()
化简得![]()
![]()
(2)总运费不超过900,即![]() 代入(1)结果得
代入(1)结果得
![]()
解得![]()
又因为x为非负整数
∴![]()
即如下三种方案
方案一:甲调往![]() :10辆;乙往
:10辆;乙往![]() :0辆;甲调往
:0辆;甲调往![]() :2辆;乙调往
:2辆;乙调往![]() :6辆.
:6辆.
方案二:甲调往![]() :9辆;乙往
:9辆;乙往![]() :1辆;甲调往
:1辆;甲调往![]() :3辆;乙调往
:3辆;乙调往![]() :5辆.
:5辆.
方案三:甲调往![]() :8辆;乙往
:8辆;乙往![]() :2辆;甲调往
:2辆;甲调往![]() :4辆;乙调往
:4辆;乙调往![]() :4辆.
:4辆.
(3)总运费![]() ,其中
,其中![]()
∵![]()
∴![]() 随
随![]() 的增大而增大
的增大而增大
∴当![]() 取最小时,运费
取最小时,运费![]() 最小
最小
代入![]() 得
得![]()
∴方案为(2)中方案1:甲往![]() :10辆;乙往
:10辆;乙往![]() :0辆;
:0辆;
甲往![]() :2辆;乙往
:2辆;乙往![]() :6辆.
:6辆.
总运费最少为860元.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知A(0,2),B(1,0), C(3,4).
(1)在坐标系中秒出个点,画出三角形ABC;再把三角形ABC先向左平移4个单位长度,再向下平移3个单位长度的三角形![]() 。
。
(2)求三角形ABC的面积;
(3)设点P在x轴上,且三角形ABP与三角形ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上的三点.
(1)请画出△ABC关于x轴对称的△ABC;
(2)请写出B点关于y轴对称的点B2的坐标;若将点B向上平移h个单位,欲使其落在△A1B1C1内部,指出h的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场以同样价格出售同样的商品:并且又各自推出不同的优惠方案,在甲商场累计购物超过100元后,超出100元的部分按![]() 收费;在乙商场累计购物超过50元后,超出50元的部分按
收费;在乙商场累计购物超过50元后,超出50元的部分按![]() 收费.顾客到哪家商场购物花费少?
收费.顾客到哪家商场购物花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
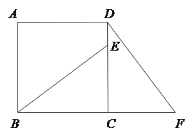
【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com