
如图,已知⊙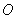 的半径为9cm,射线
的半径为9cm,射线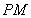 经过点
经过点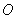 ,OP=15 cm,射线
,OP=15 cm,射线 与⊙
与⊙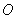 相切于点
相切于点 .动点
.动点 自P点以
自P点以 cm/s的速度沿射线
cm/s的速度沿射线 方向运动,同时动点
方向运动,同时动点 也自P点以2cm/s的速度沿射线
也自P点以2cm/s的速度沿射线 方向运动,则它们从点
方向运动,则它们从点 出发??????? s后
出发??????? s后 所在直线与⊙
所在直线与⊙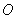 相切.
相切.

0.5s或10.5s.
【解析】
试题分析:PN与⊙O相切于点Q,OQ⊥PN,即∠OQP=90°,在直角△OPQ中根据勾股定理就可以求出PQ的值,过点O作OC⊥AB,垂足为C.直线AB与⊙O相切,则△PAB∽△POQ,根据相似三角形的对应边的比相等,就可以求出t的值.
试题解析: 连接OQ,
∵PN与⊙O相切于点Q,
∴OQ⊥PN,即∠OQP=90°,
∵OP=15,OQ=9,
∴PQ=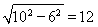 (cm).
(cm).
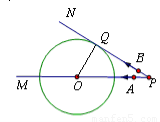
过点O作OC⊥AB,垂足为C,
∵点A的运动速度为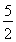 cm/s,点B的运动速度为2cm/s,运动时间为ts,
cm/s,点B的运动速度为2cm/s,运动时间为ts,
∴PA=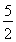 t,PB=2t,
t,PB=2t,
∵PO=15,PQ=12,
∴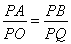 ,
,
∵∠P=∠P,
∴△PAB∽△POQ,
∴∠PBA=∠PQO=90°,
∵∠BQO=∠CBQ=∠OCB=90°,
∴四边形OCBQ为矩形.
∴BQ=OC.
∵⊙O的半径为,
∴BQ=OC=9时,直线AB与⊙O相切.
①当AB运动到如图1所示的位置,
BQ=PQ-PB=12-2t,
∵BQ=9,
∴8-4t=9,
∴t=0.25(s).
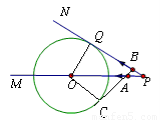
②当AB运动到如图2所示的位置,
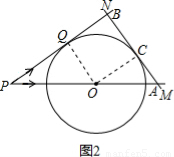
BQ=PB-PQ=2t-12,
∵BQ=9,
∴2t-12=9,
∴t=10.5(s).
∴当t为0.5s或10.5s时直线AB与⊙O相切.
考点: 1.切线的判定;2.勾股定理;3.矩形的性质;4.相似三角形的判定与性质.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com