
 ,即用a、b、
,即用a、b、 来表示CD.(提示:sin2
来表示CD.(提示:sin2 +cos2
+cos2 =1)
=1)
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N. 时,求
时,求 的值;
的值; 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
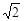 ≈1.414,
≈1.414,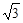 ≈1.732)
≈1.732)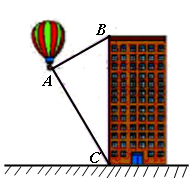
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
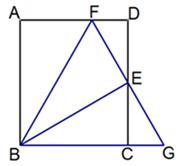
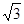 ,S△CGE=6
,S△CGE=6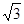 ,求AD的长。
,求AD的长。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236,
≈2.236, ≈2.449)
≈2.449)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
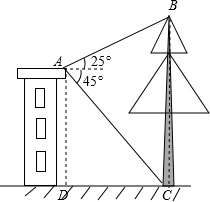
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com