
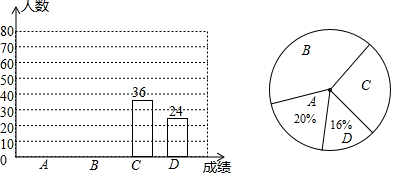
分析 (1)根据频数÷百分比=数据总数得出总人数,再分别计算A和B的人数;
(2)超过30个的有C和D,计算两组的百分比的和,与3000相乘即可;
(3)根据在“提笔忘字”现象越发严重的今天,由央视推出的《中国汉字听写大会》唤醒了国民对汉字文化的学习,这一主题,并针对学生成绩不好谈谈感想.
解答 解:(1)24÷16%=150(名)
即本次抽取的学生人数为50名;
A:20%×150=30(名),
B:150-30-36-24=60(名),
补全的条形统计图如下: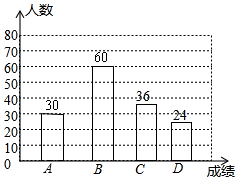
(2)3000×($\frac{36}{150}$+36%)=1200(名)
答:估计该校学生中汉字听写的成绩超过30个的学生人数有1200名;
(3)根据统计图提供的信息发现:九年级学生的听写能力普遍较低,书写水平令人担忧,给现在的语文教学敲响的警钟,从现在开始重视汉字书写,并注意笔画字形的正确性.
点评 本题考查了利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:选择题
| A. | 数据3、5、4、1、-2的中位数是3 | |
| B. | 数据1、1、0、2、4的平均数是2 | |
| C. | 在选举中,人们通常最关心是数据的众数 | |
| D. | 甲乙两人近5次数学考试平均分都是95分,方差分别是2.5和8.5,要选一人参加数学竞赛,选甲比较合适 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
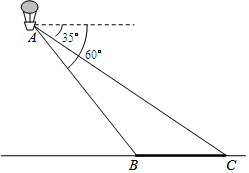 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.
如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com