
 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
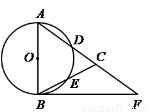
(1)求证:∠CBF=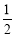 ∠CAB. (2)若AB=5,sin∠CBF=
∠CAB. (2)若AB=5,sin∠CBF=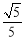 ,求BC和BF的长.
,求BC和BF的长.
(1)证明略;(2)BC= ,BF=
,BF= .
.
【解析】
试题分析:(1)连结AE.有AB是⊙O的直径可得∠AEB=90°再有BF是⊙O的切线可得BF⊥AB,利用同角的余角相等即可证明;
(2)在Rt△ABE中有三角函数可以求出BE,又有等腰三角形的三线合一可得BC=2BE,
过点C作CG⊥AB于点G.可求出AE,再在Rt△ABE中,求出sin∠2,cos∠2.然后再在Rt△CGB中求出CG,最后证出△AGC∽△ABF有相似的性质求出BF即可.
试题解析:

(1)证明:连结AE.∵AB是⊙O的直径, ∴∠AEB=90°,∴∠1+∠2=90°.
∵BF是⊙O的切线,∴BF⊥AB, ∴∠CBF +∠2=90°.∴∠CBF =∠1.
∵AB=AC,∠AEB=90°, ∴∠1= ∠CAB.
∠CAB.
∴∠CBF= ∠CAB.
∠CAB.

(2)【解析】
过点C作CG⊥AB于点G.∵sin∠CBF= ,∠1=∠CBF, ∴sin∠1=
,∠1=∠CBF, ∴sin∠1= .
.
∵∠AEB=90°,AB=5. ∴BE=AB·sin∠1=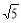 .
.
∵AB=AC,∠AEB=90°, ∴BC=2BE= .
.
在Rt△ABE中,由勾股定理得 .
.
∴sin∠2= ,cos∠2=
,cos∠2= .
.
在Rt△CBG中,可求得GC=4,GB=2. ∴AG=3.
∵GC∥BF, ∴△AGC∽△ABF. ∴ ,
,
∴ .
.
考点:切线的性质,相似的性质,勾股定理.


科目:初中数学 来源:2014-2015学年福建省福鼎市十校教研联合体九年级上学期期中联考数学试卷(解析版) 题型:解答题
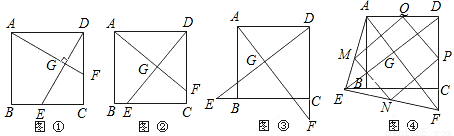
如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福鼎市十校教研联合体九年级上学期期中联考数学试卷(解析版) 题型:选择题
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )

A.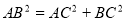 B.
B.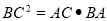
C.  D.
D. 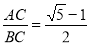
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福鼎市十校教研联合体九年级上学期期中联考数学试卷(解析版) 题型:选择题
方程x2=9的根是( )
A.x=3 B.x=-3 C. D.
D.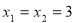
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市门头沟区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底的俯角为60°,热气球与高楼的水平距离AD 为20m,求这栋楼的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市怀柔区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角
∠ACD=60°.求接线柱AB的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省八年级12月监测数学试卷(解析版) 题型:计算题
分解因式:(每小题4分,共16分)
(1) ﹣2a2+4a﹣2 (2) (x+y)2+2(x+y)+1.
(3)3x-12x3; (4)9a2(x-y)+4b2(y-x);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com