
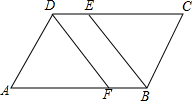
 已知,如图,在?ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE.
已知,如图,在?ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE. 科目:初中数学 来源: 题型:选择题
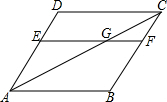 如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
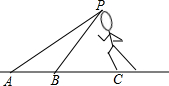 北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)
北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 最大值 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
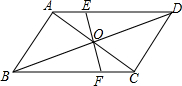 如图,?ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F,已知AB=4,BC=5,OE=1.
如图,?ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F,已知AB=4,BC=5,OE=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com