
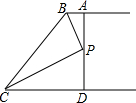
 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是4.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是4.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.| 分数段 (分数为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x<90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.
完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组号 | 分值 | 频数 |
| 一 | 6≤m<7 | 2 |
| 二 | 7≤m<8 | 8 |
| 三 | 8≤m<9 | a |
| 四 | 9≤m≤10 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
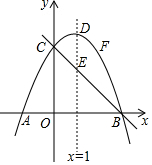 如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.
如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
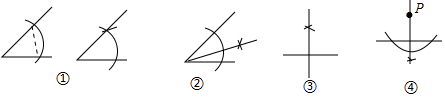
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com