
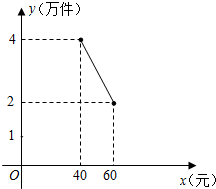
 为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.分析 (1)从图中得出40≤x≤60时,函数经过两点,使用待定系数法即可求出函数关系式;
(2)利用(1)中的函数关系,当销售单价定为50元时,可计算出月销售量,设可安排员工m人,利润=销售额一生产成本-员工工资-其它费用,列出方程即可解;
(3)先得出利润的最大值,即可求解.
解答 解:(1)当40≤x≤60时,令y=kx+b,
则$\left\{\begin{array}{l}{40k+b=4}\\{60k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=8}\end{array}\right.$,
故y=-$\frac{1}{10}$x+8;
(2)设公司可安排员工a人,定价50元时,
由5=(-$\frac{1}{10}$×50+8)(50-40)-15-0.4a,
得30-15-0.4a=5,
解得a=25,
所以公司可安排员工25人;
(3)当40≤x≤60时,
利润w1=(-$\frac{1}{10}$x+8)(x-40)-15-12=-$\frac{1}{10}$(x-60)2+13,
则当x=60时,wmax=13万元;
设该公司n个月后还清贷款,则13n≥80,
∴n≥$\frac{80}{13}$,即n=7为所求.
点评 本题主要考查学生利用待定系数法求解一次函数关系式,一次函数与一次不等式的应用,是一道综合性较强的代数应用题,能力要求比较高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | -1 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
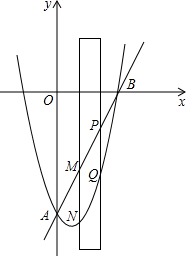 如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).
如图,抛物线y=x2+bx+c交y轴于点A(0,-8),交x轴正半轴于点B(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com