
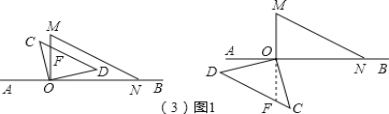
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°
(1)观察猜想
将图1中的三角尺OCD沿AB的方向平移至图②的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN= 度.
(2)操作探究
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数;
(3)深化拓展
将图1中的三角尺OCD绕点O按沿顺时针方向旋转一周,在旋转的过程中,若边CD恰好与边MN平行,请你求出此时旋转的角度.

【答案】(1)105°;(2)∠CEN=150°;(3)75![]() 或255
或255![]() .
.
【解析】
(1)根据三角形的内角和定理列式计算即可得解;
(2)由OD平分∠MON,得∠DON=![]() ∠MPN=45°,则∠DON=∠D=45°,可得CD∥AB, 由两直线平行,同旁内角互补,可得出∠CEN=150°;
∠MPN=45°,则∠DON=∠D=45°,可得CD∥AB, 由两直线平行,同旁内角互补,可得出∠CEN=150°;
(3)分当CD在AB上方及当CD在AB的下方两种情况进行讨论,画出具体图形,进行计算即可。
(1)∵∠ECN=45°,∠ENC=30°,
∴∠CEN=180![]() -75
-75![]() =105°.故答案为:105°.
=105°.故答案为:105°.
(2)∵OD平分∠MON,
∴∠DON=![]() ∠MPN=
∠MPN=![]() ×90°=45°,
×90°=45°,
∴∠DON=∠D=45°,
∴CD∥AB,
∴∠CEN=180°﹣∠MNO=180°﹣30°=150°;
(3)如图1,CD在AB上方时,设OM与CD相交于F,
∵CD∥MN,
∴∠OFD=∠M=60°,
在△ODF中,∠MOD=180°﹣∠D﹣∠OFD,
=180°﹣45°﹣60°,
=75°,
当CD在AB的下方时,设直线OM与CD相交于F,
∵CD∥MN,
∴∠DFO=∠M=60°,
在△DOF中,∠DOF=180°﹣∠D﹣∠DFO=180°﹣45°﹣60°=75°,
∴旋转角为75°+180°=255°,
综上所述,旋转的角度为75°或255°时,边CD恰好与边MN平行.
故答案为:75![]() 或255
或255![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l1:y=2x+8与坐标轴分别交于A,B两点,点C在x正半轴上,且OA=OC.点P为线段AC(不含端点)上一动点,将线段OP绕点O逆时针旋转90°,得线段OQ(见图2)
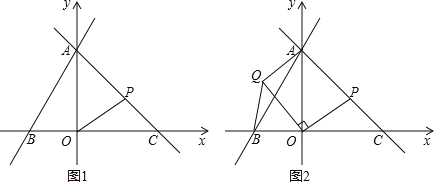
(1)分别求出点B、点C的坐标;
(2)如图2,连接AQ,求证:∠OAQ=45°;
(3)如图2,连接BQ,试求出当线段BQ取得最小值时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() (
(![]() 为常数).
为常数).
(1)求这个二元一次方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,设
,设![]() ,且m为正整数,求m的值.
,且m为正整数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE等于 _________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道:截止到2013年12月31日我国微信用户规模已达到6亿.以下是根据相关数据制作的统计图表的一部分:
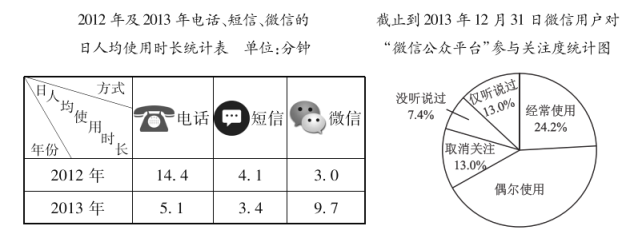
请根据以上信息,回答以下问题:
(1)从2012年到2013年微信的日人均使用时长增加了 分钟;
(2)截止到2013年12月31日,在我国6亿微信用户中偶尔使用微信用户约为 亿(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
(1)如果⊙O的半径为4,CD=![]() ,求∠BAC的度数;
,求∠BAC的度数;
(2)若点E为弧ADB的中点,连接OE,CE.求证:CE平分∠OCD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com