
【题目】如下图,正方形ABCD的边AB在x轴上,A(﹣4,0),B(﹣2,0),定义:若某个抛物线上存在一点P,使得点P到正方形ABCD四个顶点的距离相等,则称这个抛物线为正方形ABCD的“友好抛物线”.若抛物线y=2x2﹣nx﹣n2﹣1是正方形ABCD的“友好抛物线”,则n的值为_____.

科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
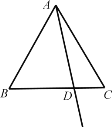
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程(a+1)x2﹣ax+a2﹣a﹣2=0的一个根与方程(a+1)x2+ax﹣a2+a+2=0的一个根互为相反数,那么(a+1)x2+ax﹣a2+a+2=0的根是( )
A. 0,﹣![]() B. 0,
B. 0,![]() C. ﹣1,2 D. 1,﹣2
C. ﹣1,2 D. 1,﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位运动员在相同条件下各射靶![]() 次,每次射靶的成绩如下:
次,每次射靶的成绩如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,长方形![]() 的项点
的项点![]() 的坐标是
的坐标是![]() .
.

(1)直接写出![]() 点坐标(______,______),
点坐标(______,______),![]() 点坐标(______,______);
点坐标(______,______);
(2)如图,D为![]() 中点.连接
中点.连接![]() ,
,![]() ,如果在第二象限内有一点
,如果在第二象限内有一点![]() ,且四边形
,且四边形![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求满足条件的点
倍,求满足条件的点![]() 的坐标;
的坐标;

(3)如图,动点![]() 从点
从点![]() 出发,以每钞
出发,以每钞![]() 个单位的速度沿线段
个单位的速度沿线段![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发.以每秒
出发.以每秒![]() 个单位的連度沿线段
个单位的連度沿线段![]() 运动,当
运动,当![]() 到达
到达![]() 点时,
点时,![]() ,
,![]() 同时停止运动,运动时间是
同时停止运动,运动时间是![]() 秒
秒![]() ,在
,在![]() ,
,![]() 运动过程中.当
运动过程中.当![]() 时,直接写出时间
时,直接写出时间![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
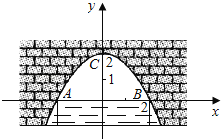
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;

(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D为
,点D为![]() 的中点,直角
的中点,直角![]() 绕点D旋转,
绕点D旋转,![]() ,
,![]() 分别与边
分别与边![]() ,
,![]() 交于E,F两点,下列结论:①
交于E,F两点,下列结论:①![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是( ).
,其中正确结论是( ).

A.①②④B.②③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com