
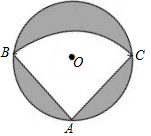
 有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.分析 (1)由∠BAC=90°,得BC为⊙O的直径,即BC=1m;又由AB=AC,得到AB=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$,而S阴影部分=S⊙O-S扇形ABC,然后根据扇形和圆的面积公式进行计算即可;
(2)扇形的半径是AB=$\frac{\sqrt{2}}{2}$,扇形BAC的弧长l=$\frac{90π×\frac{\sqrt{2}}{2}}{180}$=$\frac{\sqrt{2}}{4}$π,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
解答 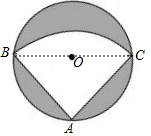 解:(1)如图,连接BC,
解:(1)如图,连接BC,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=1m,
又∵AB=AC,
∴AB=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$.
∴S阴影部分=S⊙O-S扇形ABC=π×($\frac{1}{2}$)2-$\frac{90π×(\frac{\sqrt{2}}{2})^{2}}{360}$=$\frac{π}{8}$(平方米);
(2)设底面圆的半径为r,则$\frac{90π×\frac{\sqrt{2}}{2}}{180}$=2πr,
∴r=$\frac{\sqrt{2}}{8}$m
圆锥的底面圆的半径长为$\frac{\sqrt{2}}{8}$米.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{r}^{2}}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.也考查了90度的圆周角所对的弦为直径以及等腰直角三角形三边关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
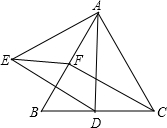 如图,已知在等边△ABC中,AD,CF分别为边CB,BA上的中线,以AD为边作等边△ADE.求证:
如图,已知在等边△ABC中,AD,CF分别为边CB,BA上的中线,以AD为边作等边△ADE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:
在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
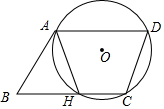 如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.
如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com