
 (2013•高要市二模)如图,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于B,大圆的弦BC⊥AB,过点C作大圆的切线交AB的延长线于D,OC交小圆于E.
(2013•高要市二模)如图,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于B,大圆的弦BC⊥AB,过点C作大圆的切线交AB的延长线于D,OC交小圆于E.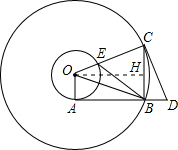 ∵∠OAB=∠ABC=∠BHO=90°,
∵∠OAB=∠ABC=∠BHO=90°,| OB2-OA2 |
| x2-1 |
| CD |
| OB |
| CB |
| AB |
| y |
| x |
| 2 | ||
|
| 2x | ||
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
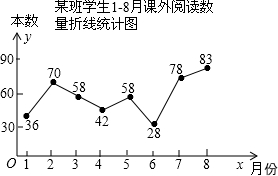 (2013•高要市二模)九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,阅读数量变化率最大的两个月是( )
(2013•高要市二模)九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,阅读数量变化率最大的两个月是( )查看答案和解析>>
科目:初中数学 来源: 题型:
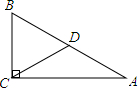 (2013•高要市二模)如图,在△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连结CD.若AC=
(2013•高要市二模)如图,在△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连结CD.若AC=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com