
【题目】已知,如图,在三角形![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时点
;同时点![]() 由
由![]() 点出发,沿
点出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 的动直线
的动直线![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,设运动时间为
,设运动时间为![]()
![]() ,解答下列问题:
,解答下列问题:

(1)线段![]() _________
_________![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 为何值时,以
为何值时,以![]() 为顶点的四边形为平行四边形?
为顶点的四边形为平行四边形?
【答案】(1)12;(2)证明见详解;(3)![]() 或t=4s.
或t=4s.
【解析】
(1)由勾股定理求出AD即可;
(2)由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB,再由等腰三角形的判定定理即可得出结论;
(3)分两种情况:①当点M在点D的上方时,根据题意得:PQ=BP=t,AM=4t,AD=12,得出MD=AD-AM=12-4t,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可;
②当点M在点D的下方时,根据题意得:PQ=BP=t,AM=4t,AD=12,得出MD=AM-AD=4t-12,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可.
(1)解:∵BD⊥AC,
∴∠ADB=90°,
∴![]() (cm),
(cm),
(2)如图所示:
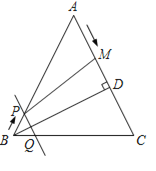
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
(3)分两种情况:
①当点M在点D的上方时,如图2所示:
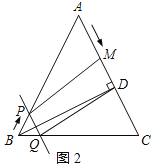
根据题意得:PQ=BP=t,AM=4t,AD=12,
∴MD=AD-AM=12-4t,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=12-4t,时,四边形PQDM是平行四边形,
解得:![]() (s);
(s);
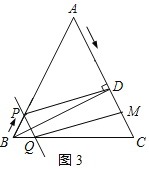
②当点M在点D的下方时,如图3所示:
根据题意得:PQ=BP=t,AM=4t,AD=12,
∴MD=AM-AD=4t-12,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=4t-12时,四边形PQDM是平行四边形,
解得:t=4(s);
综上所述,当![]() 或t=4s时,以P、Q、D、M为顶点的四边形为平行四边形.
或t=4s时,以P、Q、D、M为顶点的四边形为平行四边形.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数![]() 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.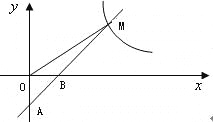
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一次函数![]() 的图象分别交x轴、y轴于点A,B,与反比例函数
的图象分别交x轴、y轴于点A,B,与反比例函数![]() 图象在第二象限交于点C(m,6),
图象在第二象限交于点C(m,6),![]() 轴于点D,OA=OD.
轴于点D,OA=OD.
(1)求m的值和一次函数的表达式;
(2)在X轴上求点P,使△CAP为等腰三角形(求出所有符合条件的点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的![]() ,则梯子比较稳定,如图,AB为一长度为6米的梯子.
,则梯子比较稳定,如图,AB为一长度为6米的梯子.
(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?
(2)如图2,若梯子底端向左滑动(3![]() ﹣2)米,那么梯子顶端将下滑多少米?
﹣2)米,那么梯子顶端将下滑多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com