
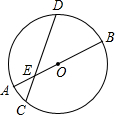
 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.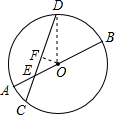 解:过O作OF⊥CD,交CD于点F,连接OD,
解:过O作OF⊥CD,交CD于点F,连接OD, OE=1,
OE=1, =
= ,
, .
.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
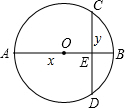 图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式
图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式查看答案和解析>>
科目:初中数学 来源:2009-2010学年安徽省铜陵市第四中学九年级(上)月考数学试卷(12月份)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《不等式与不等式组》(02)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2009年江苏省宿迁市宿豫区教育调研数学试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2008年浙江省台州市中考数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com