
分析 (1)首先把各个二次根式化简,再合并即可;
(2)先算乘除法,再化成最简二次根式,然后合并即可.
解答 解:(1)$\sqrt{16}$+6$\sqrt{\frac{1}{3}}$+$\frac{1}{\sqrt{2}-1}$=4+2$\sqrt{3}$+$\sqrt{2}$+1=5+2$\sqrt{3}$+$\sqrt{2}$;
(2)$\sqrt{6}$×2$\sqrt{2}$-$\sqrt{54}$÷$\sqrt{2}$=2$\sqrt{12}$-$\sqrt{27}$=4$\sqrt{3}$-3$\sqrt{3}$=$\sqrt{3}$.
点评 本题看成了二次根式的混合运算;把二次根式化成最简二次根式是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
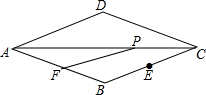 如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )| A. | 3 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-1=-3 | B. | (a4)2=a8 | C. | a6÷a2=a3 | D. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com