
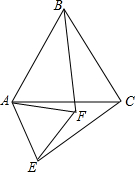
 如图,已知△ABC和△AEF都是等边三角形,求证:BF=CE.
如图,已知△ABC和△AEF都是等边三角形,求证:BF=CE. 分析 利用等边三角形的三边相等和各角都是60°,可证得△ABF≌△ACE,即可得出结论.
解答 证明:∵△ABC和△AEF都是等边三角形,
∴AB=AC,AE=AF,∠BAC=∠EAF=60°,
∵∠BAC+∠CAF=∠EAF+∠CAF,
∴∠BAF=∠CAE,
在△ABF和△ACE中,
$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAF=∠CAE}&{\;}\\{AF=AE}&{\;}\end{array}\right.$,
∴△ABF≌△ACE(SAS),
∴BF=CE.
点评 本题考查了等边三角形的性质与全等三角形的判定与性质,正确的利用等边三角形中隐含的条件证明三角形全等是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知实数a,b在数轴上位置如图所示,化简$|a|-\sqrt{b^2}+\sqrt{{{({a-b})}^2}}-\sqrt{4{a^2}}$.
已知实数a,b在数轴上位置如图所示,化简$|a|-\sqrt{b^2}+\sqrt{{{({a-b})}^2}}-\sqrt{4{a^2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE
如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,二次函数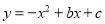 的图象经过坐标原点,与
的图象经过坐标原点,与 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com