
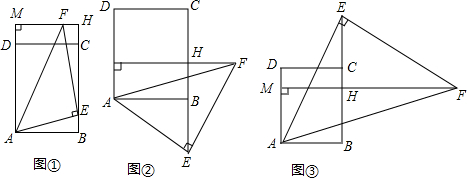
���� ��1����֤����ABE�ա�CHF������AB=HE����AM=HE����֤�ý��ۣ�
��2����֤����ABE�ա�EHF���ɵõ�AB=EH���ɵõ�AM+BE=AB��
��3����֤����ABE�ա�EHF���ɵõ�AB=HE����ɵ�AM+AB=BE�������BE�ij���
��4���ɷ���֪����AFM=15��ʱ��ֻ����ͼ2��ͼ3����ͼ2�У�����á�BAE=30�㣬��ͼ3�п���á�AEB=30�㣬�����AB�ij�����������Ӧ�Ĺ�ϵʽ�����AM��ֵ��
��� ��1��֤����
�ߡ�AEFΪ����ֱ�������Σ�
��AE=EF��
���ı���ABCDΪ���Σ�
���B=��ECD=90�㣬
���AEB+��EAB=��AEB+��FEH=90�㣬
���EAB=��FEH��
��MH��CD��
���FHE=��B=90�㣬
�ڡ�ABE�͡�CHF��
$\left\{\begin{array}{l}{��B=��EHF}\\{��EAB=��FEH}\\{AE=EF}\end{array}\right.$
���ABE�ա�CHF��AAS����
��AB=HE��
��AM=BH��
��AB+BE=BE+HE=BH=AM��
��2���⣺ͬ��1����֪AE=EF����FHE=��ABE=90�㣬
���BAE+��AEB=��AEB+��HEF=90�㣬
���BAE=��HEF��
�ڡ�ABE�͡�CHF��
$\left\{\begin{array}{l}{��BAE=��HEF}\\{��ABE=��FHE}\\{AE=EF}\end{array}\right.$
���ABE�ա�CHF��AAS����
��AB=HE��
��AM=BH��
��AB-BE=HE-BE=HB=AM��
��3���⣺ͬ��1����֪AE=EF����FHE=��ABE=90�㣬
���BAE+��AEB=��AEB+��HEF=90�㣬
���BAE=��HEF��
�ڡ�ABE�͡�CHF��
$\left\{\begin{array}{l}{��BAE=��HEF}\\{��ABE=��FHE}\\{AE=EF}\end{array}\right.$
���ABE�ա�CHF��AAS����
��AB=HE��
��AM=BH��
��AB+AM=HE+BH=BE��
��AB=4��AM=3��
��BE=AB+AM=7��
��4���⣺
��E�����߶�BC��ʱ��
��MH��AB��
���FAB=��AFM=45��+��EAB��15�㣬��E�㲻�����߶�BC�ϣ�
�ٵ���E���߶�CB���ӳ�����ʱ�����С�AFM=��FAB=15�㣬
�ߡ�FAE=45�㣬
���BAE=30�㣬���AEB=60�㣬
��AB=BE•tan60��=3$\sqrt{3}$��
��AM=AB-BE=3$\sqrt{3}$-3��
�ڵ���E�ڱ�BC���ӳ�����ʱ��ͬ������á�AEB=30�㣬
��ʱ��AB=BE•tan30��=3��$\frac{\sqrt{3}}{3}$=$\sqrt{3}$��
��AM=BE-AB=3-$\sqrt{3}$��
���Ͽ�֪��BE=3����AFM=15��ʱ��AM��ֵΪ3$\sqrt{3}$-3��3-$\sqrt{3}$��
���� ����Ϊ�ı��ε��ۺ�Ӧ�ã��漰֪ʶ���е��������ε����ʡ����ε����ʡ�ȫ�������ε��ж������ʡ����Ǻ����Ķ��弰��������˼��ȣ��ڽ��ÿһ��ʱ��֤��������ȫ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
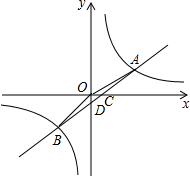 ��֪����ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������$y=\frac{k}{x}��k��0��$��ͼ����һ���������ڵ�A��B���㣬��x���ڵ�C����y�ύ�ڵ�D��OC=1��BC=5��$sin��BCO=\frac{3}{5}$��
��֪����ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������$y=\frac{k}{x}��k��0��$��ͼ����һ���������ڵ�A��B���㣬��x���ڵ�C����y�ύ�ڵ�D��OC=1��BC=5��$sin��BCO=\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
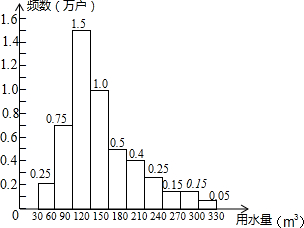 Ϊ�˽�Լˮ��Դ��ij�������վ����ͥ����ˮ��ʵ�н���ˮ�ۣ�ˮ�۷ֵ��������ƻ�ʹ��һ�����ڶ����͵�������ˮ�۷ֱ�ȫ�о����ͥ��80%��15%��5%��Ϊ����ȷ������֮��Ľ��ޣ��������˸���5�����ͥ��һ�������ˮ������λ��m3����������ͳ��ͼ����ͼ��ʾ�������ĸ��ƶϺ������ǣ�������
Ϊ�˽�Լˮ��Դ��ij�������վ����ͥ����ˮ��ʵ�н���ˮ�ۣ�ˮ�۷ֵ��������ƻ�ʹ��һ�����ڶ����͵�������ˮ�۷ֱ�ȫ�о����ͥ��80%��15%��5%��Ϊ����ȷ������֮��Ľ��ޣ��������˸���5�����ͥ��һ�������ˮ������λ��m3����������ͳ��ͼ����ͼ��ʾ�������ĸ��ƶϺ������ǣ�������| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com