
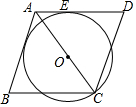
 如图,点O在菱形ABCD的对角线AC上,以OC为半径的⊙O与边AD相切于点E.
如图,点O在菱形ABCD的对角线AC上,以OC为半径的⊙O与边AD相切于点E.分析 (1)如图1中,连接OE,作OF⊥AB于F.只要证明OE=OF即可.
(2)如图1中,设⊙的半径为r,由∠B=60°,BC∥AD,推出∠B+∠BAD=180°,推出∠BAD=120°,推出∠OAE=∠BAC=$\frac{1}{2}$∠BAD=60°,推出△ABC是等边三角形,推出AB=AB=6,在Rt△AOE中,sin60°=$\frac{OE}{OA}$,推出OA=$\frac{r}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$r,可得$\frac{2\sqrt{3}}{3}$r+r=6,解方程即可.
(3)如图2中,连接EF、FG、EH、OE、OF、OG、OH.通过计算只要证明∠EOF=∠FOG=∠GOC=∠COH=∠HOE=72°即可解决问题.
解答 (1)证明:如图1中,连接OE,作OF⊥AB于F.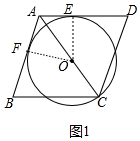
∵四边形ABCD是菱形,
∴CA平分∠BAD,
∵⊙O与AD相切于点E,
∴OE⊥AD,∵OF⊥AB,
∴OE=OF,
∴直线AB与⊙O相切.
(2)解:如图1中,设⊙的半径为r,
∵∠B=60°,BC∥AD,
∴∠B+∠BAD=180°,
∴∠BAD=120°,
∴∠OAE=∠BAC=$\frac{1}{2}$∠BAD=60°,
∴△ABC是等边三角形,
∴AB=AB=6,
在Rt△AOE中,sin60°=$\frac{OE}{OA}$,
∴OA=$\frac{r}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$r,
∴$\frac{2\sqrt{3}}{3}$r+r=6,
∴r=12$\sqrt{3}$-18.
(3)证明:如图2中,连接EF、FG、EH、OE、OF、OG、OH.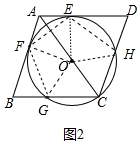
∵四边形ABCD是菱形,
∴∠BAD=∠BCD=108°,
∴∠ACB=∠ACD=∠CAF=∠CAD=54°,
∵OG=OC=OH,
∴∠OGC=∠OCG=∠OCH=∠OHC=54°,
∴∠GOC=∠OCH=72°,
在四边形AFOE中,∠EOF=360°-∠AEO-∠AFO-∠EAF=72°,
∴∠AOF=∠AOE=36°,
∴∠FOG=∠EOH=180°-36°-72°=72°,
∴∠EOF=∠FOG=∠GOC=∠COH=∠HOE=72°,
∴四边形EFGCH是正五边形.
点评 本题考查圆综合题.角平分线的性质定理、切线的性质、菱形的性质、锐角三角函数、等边三角形的判定和性质、正五边形的判定等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,掌握正五边形的证明方法,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
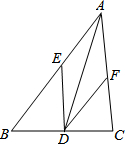 如图,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
如图,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
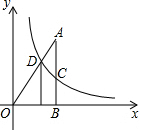 如图,过点A(3,4)作AB⊥x轴,垂足为B,交反比例函数y=$\frac{k}{x}$的图象于点C(x1,y1),连接OA交反比例函数y=$\frac{k}{x}$的图象于点D(2,y2),则y2-y1=$\frac{8}{9}$.
如图,过点A(3,4)作AB⊥x轴,垂足为B,交反比例函数y=$\frac{k}{x}$的图象于点C(x1,y1),连接OA交反比例函数y=$\frac{k}{x}$的图象于点D(2,y2),则y2-y1=$\frac{8}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{7}{2}$ | B. | 2 | C. | $\frac{7}{2}$ | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
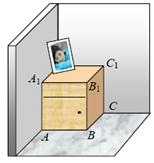 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com