
���� ��1����������=ÿ��������������������ɽ�����⣮
��2�����ã�1���н�����г����̼��ɣ�
��3�������䷽�������ɽ�����⣮
��� �⣺��1������ʱ��w=��x-40��[300+20��60-x��]=-20x2+2300x-60000��40��x��60��
��2����w=-20x2+2300x-60000=6000�����x1=55��x2=60����ȥ��
�𣺵�ÿ����Ʒ���ۼ۶�Ϊ55Ԫʱ��һ�����ڵ�����ǡ��Ϊ6000Ԫ
��3��w1=-10��x-65��2+6250��
��a=-10��0��
�൱x=65ʱ��w1�����ֵΪ6250Ԫ
w2=-20x2+2300x-60000=-20��x-57.5��2+6120
��x=57.5ʱ��w2�����ֵΪ6120Ԫ
��6250��6120
�൱ÿ����Ʒ�Ķ���Ϊ65Ԫʱ������������
���� ���⿼���˶��κ�����Ӧ�ü�һԪ���η��̵�Ӧ�ã������Ĺؼ�����ϸ���⣬��ʵ������ת��Ϊ��ѧģ����⣬ע���䷽������κ�����ֵ��Ӧ��


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
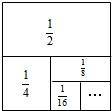 ����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ĵ�9�¡���ʽ�˷�����ʽ�ֽ⡷�ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼��������������
����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ĵ�9�¡���ʽ�˷�����ʽ�ֽ⡷�ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼���������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
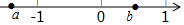 ������a��b�������϶�Ӧ��λ����ͼ��ʾ��������
������a��b�������϶�Ӧ��λ����ͼ��ʾ��������| A�� | a-b��0 | B�� | a+b��0 | C�� | a-b=0 | D�� | a-b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 7 | C�� | -5��7 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ���� | C�� | �Ǹ��� | D�� | ʵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3+a3=3a6 | B�� | ��-a��3•��-a��5=-a8 | ||
| C�� | ��-2a2b��•4a=-24a6b3 | D�� | ��-$\frac{1}{3}$a-4b����$\frac{1}{3}$a-4b��=16b2-$\frac{1}{9}$a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com