【题目】如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是_________。
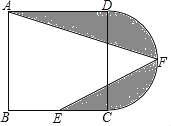
【答案】18+18π
【解析】
作FH⊥BC于H，连接AE，如图，根据正方形的性质和切线的性质得BE=CE=CH=FH=6，则利用勾股定理可计算出
，通过Rt△ABE≌△EHF得∠AEF=90°，然后利用图中阴影部分的面积=S正方形ABCD+S半圆-S△ABE-S△AEF进行计算．
解：作FH⊥BC于H，连接AE，如图，
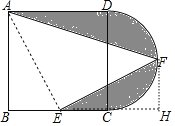
∵点E为BC的中点，点F为半圆的中点，
∴BE=CE=CH=FH=6，
，
易得Rt△ABE≌△EHF，
∴∠AEB=∠EFH，
而∠EFH+∠FEH=90°，
∴∠AEB+∠FEH=90°，
∴∠AEF=90°，
∴图中阴影部分的面积=S正方形ABCD+S半圆-S△ABE-S△AEF
=18+18π．
备战中考寒假系列答案科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD内接于⊙O，AB=AC，BD⊥AC，垂足为E，点F在BD的延长线上，且DF=DC，连接AF、CF.
(1)求证：∠BAC=2∠DAC；
(2)若AF＝10，BC＝4
，求tan∠BAD的值.
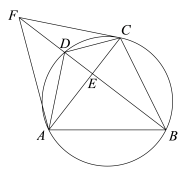
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HE与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）（参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，
≈1.732，
≈1.414）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一枚均匀的正四面体，四个面上分别标有数字1，2，3，4，小红随机地抛掷一次，把着地一面的数字记为x；另有三张背面完全相同，正面上分别写有数字－2，－1，1的卡片，小亮将其混合后，正面朝下放置在桌面上，并从中随机地抽取一张，把卡片正面上的数字记为y；然后他们计算出S=x+y的值．
(1)用树状图或列表法表示出S的所有可能情况；
(2)分别求出当S=0和S<2时的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】皮特是红树林中学的一个外籍教师，目前，他在电脑上打英语单词的平均速度是打汉字速度的2倍．某次，他连续打完一篇3600字（单词）的英语文章和一篇600字的汉语文章，一共刚好花了40分钟．（速度按每分钟打多少个英语单词或汉字测算）．
（1）皮特目前平均每分钟打多少汉字；
（2）最近，皮特把一篇汉语文章翻译成英文，原文加上译文总字数为6000字，已知它在1小时内（含1小时）打完了这6000字，问原文最多有多少汉字？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．
（1）求证：AF=DC；
（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．
（1）在图1中证明CE=CF；
（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；
（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．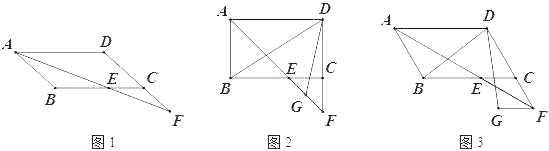
查看答案和解析>>
科目：初中数学 来源： 题型：
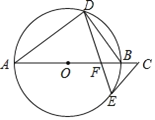
【题目】如图，AB是⊙O的直径，点D，E在⊙O上，∠A=2∠BDE，点C在AB的延长线上，∠C=∠ABD．
（1）求证：CE是⊙O的切线；
（2）若⊙O的半径长为5，BF=2，求EF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
