
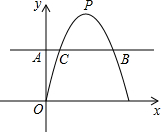
 且与直线AB交于另一点C(在B的左边),抛物线的顶点为P.
且与直线AB交于另一点C(在B的左边),抛物线的顶点为P.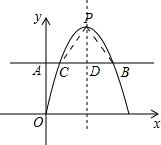 解:(1)∵A(0,a),AB=a,
解:(1)∵A(0,a),AB=a, ,
,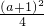 ),
),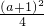 -a=
-a= ,
, BC,即
BC,即 =
= (a-1),解得a=3;
(a-1),解得a=3; BC,即
BC,即 =
= (a-1),解得a=2
(a-1),解得a=2 +1,
+1, +1时△PCB是等边三角形.
+1时△PCB是等边三角形. BC;当△PCB是等边三角形,根据等边三角形的高等于边长的
BC;当△PCB是等边三角形,根据等边三角形的高等于边长的 倍得到PD=
倍得到PD= BC,这样得到关于a的两个方程,分别解方程即可得到a的值.
BC,这样得到关于a的两个方程,分别解方程即可得到a的值. ,
, ).也考查了等腰直角三角形和等边三角形的性质.
).也考查了等腰直角三角形和等边三角形的性质. 

 互动英语系列答案
互动英语系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com