解:(1)连接PB,如图所示,
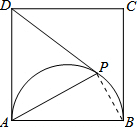
∵AB为半圆的直径,
∴∠APB=90°,
在Rt△ABP中,AB=5,∠PAB=37°,
∴cos∠PAB=

,即cos37°=0.8=
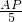
,
∴AP=4;
(2)PE为半圆的切线,理由为:
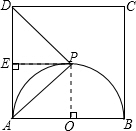
过P作PO⊥AB,设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∵PE⊥PA,PO⊥AB,
∴∠PEA=∠POA=90°,
∴四边形EAOP是矩形,
∴EA=PO,∠EPO=90°,
∵DP=AP,PE⊥DA,
∴EA=

DA=

a,
∴PO=

a,PO为半圆的半径,
∴PE为半圆的切线.
分析:(1)连接PB,由AB为半圆的直径,利用直径所对的圆周角为直角得到∠APB为直角,在直角三角形APB中,利用余弦函数定义及AB的长,即可求出PA的长;
(2)直线PE与半圆的位置关系为相切,理由为:根据题意画出相应的图形,如图所示,过P作PO⊥AB,由四边形ABCD为正方形,设正方形边长为a,得到∠DAB为直角,再由垂直的定义得到两个角为直角,利用三个角为直角的四边形是矩形得到AOPE为矩形,利用矩形的四个角为直角得到∠EPO为直角,对边相等得到AE=PO,根据DP=AP,PE垂直于AD,利用三线合一得到EA=PO=

a,进而确定出PO为圆的半径,直线PE与半圆相切.
点评:此题考查了切线的判定,矩形、正方形的判定与性质,以及锐角三角函数定义,熟练掌握切线的判定方法是解本题的关键.

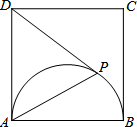 如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
 ,即cos37°=0.8=
,即cos37°=0.8=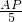 ,
,
 DA=
DA= a,
a, a,PO为半圆的半径,
a,PO为半圆的半径, a,进而确定出PO为圆的半径,直线PE与半圆相切.
a,进而确定出PO为圆的半径,直线PE与半圆相切.


 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且
