
已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,﹣4).
(1)求该二次函数的解析式;
(2)当y>﹣3,写出x的取值范围;
(3)A、B为直线y=﹣2x﹣6上两动点,且距离为2,点C为二次函数图象上的动点,当点C运动到何处时△ABC的面积最小?求出此时点C的坐标及△ABC面积的最小值.
解:(1)∵点(1,0),(5,0),(3,﹣4)在抛物线上,
∴ ,解得
,解得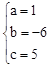 。
。
∴二次函数的解析式为:y=x2﹣6x+5。
(2)在y=x2﹣6x+5中,令y=﹣3,即x2﹣6x+5=﹣3,
整理得:x2﹣6x+8=0,解得x1=2,x2=4。
结合函数图象,可知当y>﹣3时,x的取值范围是:x<2或x>4。
(3)设直线y=﹣2x﹣6与x轴,y轴分别交于点M,点N,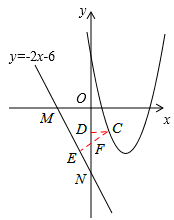
令x=0,得y=﹣6;令y=0,得x=﹣2,
∴M(﹣3,0),N(0,﹣6)。
∴OM=3,ON=6,由勾股定理得:MN=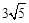 ,
,
∴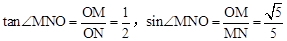 。
。
设点C坐标为(x,y),则y=x2﹣6x+5。。
过点C作CD⊥y轴于点D,
则CD=x,OD=﹣y,DN=6+y。
过点C作直线y=﹣2x﹣6的垂线,垂足为E,交y轴于点F,
在Rt△CDF中,DF=CD•tan∠MNO=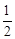 x,
x,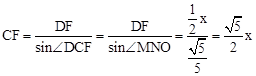 。
。
∴FN=DN﹣DF=6+y﹣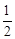 x。
x。
在Rt△EFN中,EF=FN•sin∠MNO=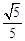 (6+y﹣
(6+y﹣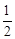 x),
x),
∴CE=CF+EF=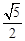 x+
x+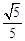 (6+y﹣
(6+y﹣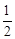 x)。
x)。
∵C(x,y)在抛物线上,
∴y=x2﹣6x+5,代入上式整理得:CE=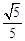 (x2﹣4x+11)=
(x2﹣4x+11)=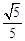 (x﹣2)2+
(x﹣2)2+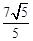 。
。
∴当x=2时,CE有最小值,最小值为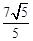 。
。
当x=2时,y=x2﹣6x+5=﹣3,∴C(2,﹣3)。
∴△ABC的最小面积为: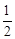 AB•CE=
AB•CE=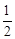 ×2×
×2×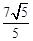 =
=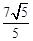 。
。
∴当C点坐标为(2,﹣3)时,△ABC的面积最小,面积的最小值为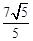 。
。
解析试题分析:(1)利用待定系数法求出抛物线的解析式。
(2)求出y=3时x的值,结合函数图象,求出y>﹣3时x的取值范围。
(3)△ABC的底边AB长度为2,是定值,因此当AB边上的高最小时,△ABC的面积最小.如解答图所示,由点C向直线y=﹣2x﹣6作垂线,利用三角函数(或相似三角形)求出高CE的表达式,根据表达式求出CE的最小值,这样问题得解。


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,顶点为M的抛物线 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形ABCD的边长AB=4米,∠ABC=60°.设AE=x米(0<x<4),矩形EFGH的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草.已知红色花草的价格为20元/米2,黄色花草的价格为40元/米2.当x为何值时,购买花草所需的总费用最低,并求出最低总费用(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年广东梅州10分)如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.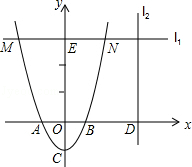
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,AB是半圆O的直径,以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D,其中OA=4.
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接OD,当OD与半圆C相切时,求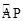 的长;
的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)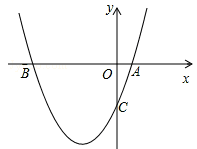
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知关于x的二次函数y=x2﹣2mx+m2+m的图象与关于x的函数y=kx+1的图象交于两点A(x1,y1)、B(x2,y2);(x1<x2)
(1)当k=1,m=0,1时,求AB的长;
(2)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.
(3)当m=0,无论k为何值时,猜想△AOB的形状.证明你的猜想.
(平面内两点间的距离公式 ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为9,则k的值为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com