
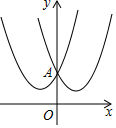
 ����������κ�����ͼ�����y��Գƣ����Ǿͳ����������κ�����Ϊ������y��Գƶ��κ���������ͼ��ʾ���κ���y1=x2+2x+2��y2=x2-2x+2�ǡ�����y��Գƶ��κ�������
����������κ�����ͼ�����y��Գƣ����Ǿͳ����������κ�����Ϊ������y��Գƶ��κ���������ͼ��ʾ���κ���y1=x2+2x+2��y2=x2-2x+2�ǡ�����y��Գƶ��κ����������� ��1�����ݡ�����y��Գƶ��κ��������ɵô𰸣�
��2�����ݡ�����y��Գƶ��κ��������ɵô𰸣�
��3�����ݡ�����y��Գƶ��κ����������ε�������ɵö������꣬ͼ����y��Ľ��㣬���ݴ���ϵ�������ɵô𰸣�
��� �⣺��1��ֱ��д������ͼ�С�����y��Գƶ��κ�����ͼ�������еĹ�ͬ�ص�ʱ�������y��Գƣ��Գ������y��Գƣ�
��2�����κ���y=2��x+2��2+1�ġ�����y��Գƶ��κ���������ʽΪ y=2��x+2��2+1��
���κ���y=a��x-h��2+k�ġ�����y��Գƶ��κ���������ʽΪy=a��x+h��2+k
�ʴ�Ϊ��y=2��x+2��2+1��y=a��x+h��2+k��
��3����ͼ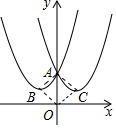 ��
��
��BC=6��˳�����ӵ�A��B��O��C�õ�һ�����Ϊ24�����Σ���
OA=8��A��������0��8����B���������-3��4����
��һ�������ߵĽ���ʽΪy=a��x+3��2+4����A��������룬��
9a+4=8��
���a=$\frac{4}{9}$��
y=$\frac{4}{9}$��x+3��2+4����y��Գƶ��κ����ĺ�������ʽy=$\frac{4}{9}$��x-3��2+4��
���� ���⿼���˴���ϵ�������������ε����ʵó�A������Ϊ��0��8����B�������Ϊ��-3��4���ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
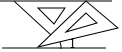 ��ͼ����һ�����ǰ��һ�ŶԱ�ƽ�е�ֽ�������з�ʽ�ڷţ��������ǰ��һֱ�DZ��غϣ���45��ǵ�ֱ�����ǰ��б����ֽ��һ���غϣ���30��ǵ����ǰ��һ��������ֽ������һ���ϣ����1�Ķ����ǣ�������
��ͼ����һ�����ǰ��һ�ŶԱ�ƽ�е�ֽ�������з�ʽ�ڷţ��������ǰ��һֱ�DZ��غϣ���45��ǵ�ֱ�����ǰ��б����ֽ��һ���غϣ���30��ǵ����ǰ��һ��������ֽ������һ���ϣ����1�Ķ����ǣ�������| A�� | 30�� | B�� | 20�� | C�� | 15�� | D�� | 14�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
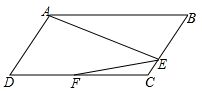 ��ͼ����֪?ABCD�У�AB=2BC��AE��BC��E��F��CD���е㣬��FEC=54�㣬���B�Ķ�����
��ͼ����֪?ABCD�У�AB=2BC��AE��BC��E��F��CD���е㣬��FEC=54�㣬���B�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
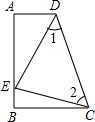 ��ͼ����A=��B=90�㣬E��AB�ϵ�һ�㣬��AE=BC����1=��2��
��ͼ����A=��B=90�㣬E��AB�ϵ�һ�㣬��AE=BC����1=��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
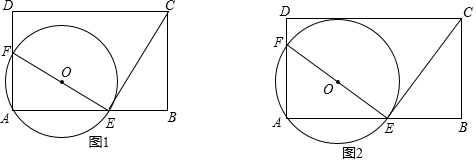
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
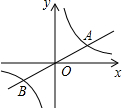 ��ֱ֪��y=$\frac{1}{2}$x��˫����y=$\frac{k}{x}$��k��0������A��B���㣬�ҵ�A�ĺ�����Ϊ4��
��ֱ֪��y=$\frac{1}{2}$x��˫����y=$\frac{k}{x}$��k��0������A��B���㣬�ҵ�A�ĺ�����Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com