
【题目】如图,等边△ABC中,点D、E、F分别是AB、AC、BC中点,点M在CB的延长线上,△DMN为等边三角形,且EN经过F点.下列结论:①EN=MF ②MB=FN ③MP·DP=NP·FP ④MB·BP=PF·FC,正确的结论有( )
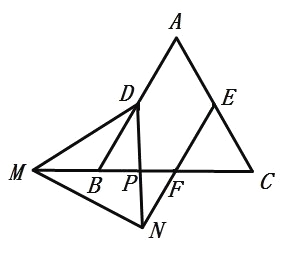
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①连接DE、DF,根据等边三角形的性质得到∠MDF=∠NDE,证明△DMF≌△DNE,根据全等三角形的性质证明;
②根据①的结论结合点D、E、F分别是AB、AC、BC中点,即可得证;
③根据题目中的条件易证得![]() ,即可得证;
,即可得证;
④根据题目中的条件易证得![]() ,再则等量代换,即可得证.
,再则等量代换,即可得证.
连接![]() ,
,

∵![]() 和
和![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∵点![]() 分别为边
分别为边![]() 的中点,
的中点,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]()
![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
故①正确;
∵点![]() 分别为等边三角形三边
分别为等边三角形三边![]() 的中点,
的中点,
∴四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
故②正确;
∵点![]() 分别为等边三角形三边
分别为等边三角形三边![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,
∴![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故③错误;
∵点![]() 分别为等边三角形三边
分别为等边三角形三边![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由②得![]() ,
,
∴![]() ,
,
∴![]() ,
,
故④正确;
综上:①②④共3个正确.
故选:C


科目:初中数学 来源: 题型:
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
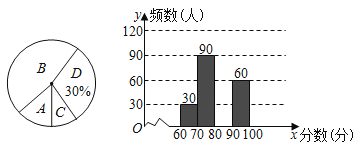
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的
为直径的![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,点
,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() .
.
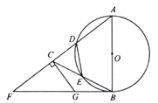
(1)试说明![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
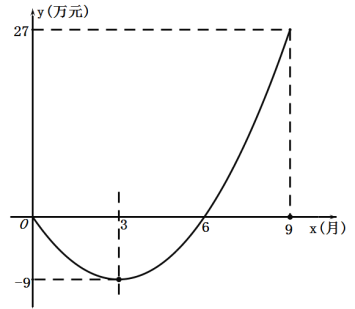
【题目】大学生小李和同学一起自主创业开办了一家公司,公司对经营的盈亏情况在每月的最后一天结算一次.在1-12月份中,该公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系.
(1)求y与x函数关系式.
(2)该公司从哪个月开始“扭亏为盈”(当月盈利)? 直接写出9月份一个月内所获得的利润.
(3)在前12 个月中,哪个月该公司所获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川是闻名天下的“熊猫之乡”,每年到大熊猫基地游玩的游客络绎不绝,大学生小张加入创业项目,项目帮助她在基地附近租店卖创意熊猫纪念品.已知某款熊猫纪念物成本为30元/件,当售价为45元/件时,每天销售250件,售价每上涨1元,销量下降10件.
(1)求每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)若每天该熊猫纪念物的销售量不低于240件的情况下,当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
(3)小张决定从这款纪念品每天的销售利润中捐出150元给希望工程,为了保证捐款后这款纪念品每天剩余利润不低于3600元,试确定该熊猫纪念物销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com