
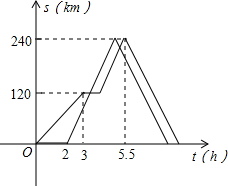
 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.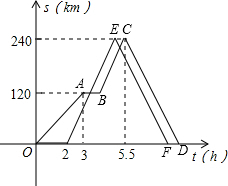
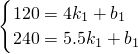 ,
,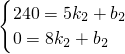 ,
, ,
,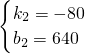 ,
,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市初中毕业学业考试模拟试卷数学卷 题型:解答题
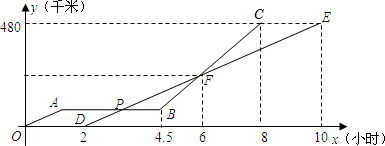
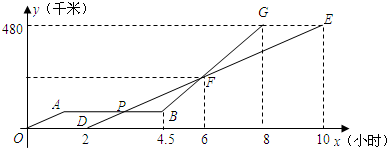
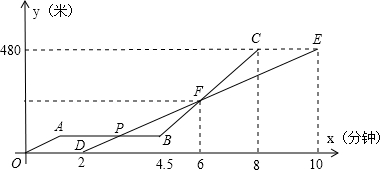
(本小题满分8分)甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线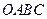 、线段
、线段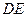 分别表示甲、乙两车所行路程
分别表示甲、乙两车所行路程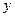 (千米)与时间
(千米)与时间 (小时)之间的函数关系对应的图象(线段
(小时)之间的函数关系对应的图象(线段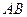 表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
(1)求乙车所行路程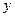 与时间
与时间 的函数关系式;
的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com