
分析 由AD、BD是方程x2-6x+4=0的两根可以得到AD+BD=6,AD•BD=4,易证△DBC∽△DCA,可得到CD=$\sqrt{AD•BD}$=2,而△ABC的面积=$\frac{1}{2}$×(AD+BD)×CD,由此可以求出面积.
解答 解:∵AD、BD是方程x2-6x+4=0的两根,
∴AD+BD=6,AD•BD=4,
∵∠ACB=90°,CD⊥AB于D,
∴△DBC∽△DCA,
∴$\frac{CD}{AD}=\frac{DB}{CD}$,
∴CD2=AD•BD,
∴CD=$\sqrt{AD•BD}$=2,
∴S△ABC=$\frac{1}{2}$×(AD+BD)×CD=6.
点评 本题考查了相似三角形的判定和性质,勾股定理,此题难点是利用相似求得斜边上的高,解题关键是得到所求三角形相应的底与高的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 在?ABCD中,对角线AC、BD相交于点O,点E、F在对角线BD上,且OE=OF.
在?ABCD中,对角线AC、BD相交于点O,点E、F在对角线BD上,且OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.
如图,在△ABC和△BCE中,∠CBE=30°,∠BEC=90°,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点F,与直线CB交于点Q,当△BPQ为等腰三角形时,α的大小是30°,75°或165°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
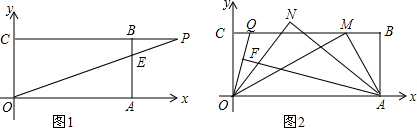
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.
如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com