
【题目】如图,在平面直角坐标系中,点A( ![]() ,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 .
,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 . 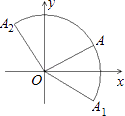
【答案】![]()
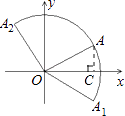
【解析】解:过点A作AC⊥x轴于点C,
∵点A的坐标为( ![]() ,1),
,1),
∴AO= ![]() =2,
=2,
∴tan∠AOC= ![]() =
= ![]() =
= ![]() ,
,
∴∠AOC=30°,
∵点A( ![]() ,1)关于x轴的对称点为点A1 ,
,1)关于x轴的对称点为点A1 ,
∴∠COA1=30°,
∵将OA绕原点O逆时针方向旋转90°到OA2 ,
∴∠A2OA1=∠AOC+∠COA1+∠A2OA=30°+90°+30°=150°,
∴圆锥底面圆的周长为: ![]() =
= ![]() =
= ![]() π,
π,
∴该圆锥的底面圆的半径为:2πR= ![]() π,
π,
∴R= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了圆锥的相关计算的相关知识点,需要掌握圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.才能正确解答此题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】小青和小白在一起玩数学游戏,他们约定:在一个不透明的布袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,小青随机摸出一个小球记下数字后放回去,小白再随机摸出一个小球记下数字.
(1)求小青和小白摸出小球标号相同的概率;
(2)如果小青和小白按照上述方式继续进行游戏,并且把他们所摸出的两个数分别看作点的横坐标和纵坐标,记作(小青,小白),当点在直线y=x+1上时,小青胜;反之则小白胜,请判断这个游戏对双方是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在边AD上,将此矩形沿CE折叠,点D落在点F处,连接BF,B、F、E三点恰好在一直线上.
(1)求证:△BEC为等腰三角形;(2)若AB=2,∠ABE=45°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(a,3),点P在坐标轴上,若使得△AOP是等腰三角形的点P恰有6个,则满足条件的a值有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.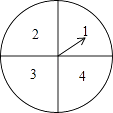
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y1=x2﹣2x﹣1与反比例函数y2=﹣ ![]() (x>0)的图象在如图所示的同一坐标系中,若y1>y2时,则x的取值范围( )
(x>0)的图象在如图所示的同一坐标系中,若y1>y2时,则x的取值范围( )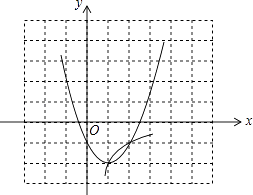
A.﹣1<x<1 或 x>2
B.1<x<2
C.x<1
D.0<x<1或x>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列题目.
(1)求:![]() +
+![]() +
+![]() +…+
+…+![]() 的值.
的值.
对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成![]() 的形式,而
的形式,而![]() =
=![]() ﹣
﹣![]() ,这样就把
,这样就把![]() 一项(分)裂成了两项.
一项(分)裂成了两项.
试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出![]() +
+![]() +
+![]() +…+
+…+![]() 的值.
的值.
(2)若![]() =
=![]() +
+![]()
①求:A、B的值:
②求:![]() +
+![]() +…+
+…+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=![]() S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com