
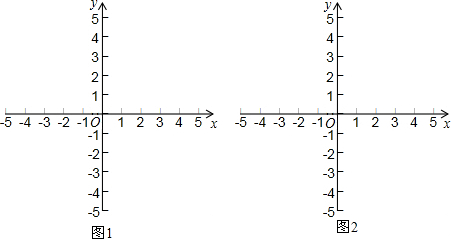
分析 (1)只需根据新定义即可解决问题;
(2)过点O作直线y=x的垂线,与双曲线y=$\frac{k}{x}$交于点A、B,过点B作BH⊥x轴,如图1,根据新定义可得直线y=x和双曲线y=$\frac{k}{x}$之间的距离就是线段OB的长,如何只需求出点B的坐标,运用待定系数法就可求出k的值;
(3)①过点O分别作射线OE、OF的垂线OG、OH,如图2,根据新定义可得图形M为y轴的正半轴、∠GOH的边及其内部所有的点;
②设抛物线y=x2-2与射线OG的交点为N,如图3,图形N上点的坐标可设为(x,x2-2),根据新定义可得图形W与图形N之间的距离为$\sqrt{{x}^{2}+({x}^{2}-2)^{2}}$的最小值.可通过求出点N的坐标得到x2的范围,然后利用二次函数的增减性求出x2+(x2-2)2=(x2-$\frac{3}{2}$)2+$\frac{7}{4}$的最小值,就可解决问题.
解答 解:(1)点(2,3)和射线OA之间的距离为3,
点(-2,3)和射线OA之间的距离为$\sqrt{(-2)^{2}+{3}^{2}}$=$\sqrt{13}$,
故答案分别为:3、$\sqrt{13}$;
(2)∵直线y=x和双曲线y=$\frac{k}{x}$之间的距离为$\sqrt{2}$,
∴k<0(否则直线y=x和双曲线y=$\frac{k}{x}$相交,它们之间的距离为0).
过点O作直线y=x的垂线,与双曲线y=$\frac{k}{x}$交于点A、B,过点B作BH⊥x轴,如图1,
在Rt△OHB中,∠HOB=∠HBO=45°,OB=$\sqrt{2}$,
则有OH=BH=$\frac{\sqrt{2}}{2}$OB=1,
∴点B的坐标为(1,-1),
∴k=1×(-1)=-1,
故答案为:-1;
(3)①过点O分别作射线OE、OF的垂线OG、OH,如图2,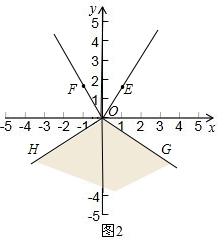
则图形M为:y轴的正半轴、∠GOH的边及其内部所有的点(图2中的阴影部分);
②图形W与图形N之间的距离为$\frac{4}{3}$.
提示:设抛物线y=x2-2与射线OG的交点为N,如图3,
图形N上点的坐标可设为(x,x2-2),
则图形W与图形N之间的距离为$\sqrt{{x}^{2}+({x}^{2}-2)^{2}}$的最小值.
易求出点N的坐标为($\frac{2\sqrt{3}}{3}$,-$\frac{2}{3}$),从而有0≤x2≤$\frac{4}{3}$,
由此可得x2+(x2-2)2=(x2-$\frac{3}{2}$)2+$\frac{7}{4}$的最小值为($\frac{4}{3}$-$\frac{3}{2}$)2+$\frac{7}{4}$=$\frac{16}{9}$,
则图形W与图形N之间的距离为$\sqrt{\frac{16}{9}}$=$\frac{4}{3}$.
点评 本题属于新定义型,考查了用待定系数法求反比例函数的解析式、抛物线的增减性、勾股定理、求直线与抛物线的交点等知识,解决本题的关键是对新定义的理解.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图所示,在平面直角坐标系中,描出下列3个点,A(-1,0),B(5,0),C(3,4);
(1)如图所示,在平面直角坐标系中,描出下列3个点,A(-1,0),B(5,0),C(3,4);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com