
【题目】在同一平面内,将两个全等的等腰直角三角形![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,若
,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合).
重合).
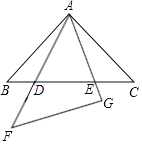
(1)求证:![]() ;
;
(2)在旋转过程中,试判断等式![]() 是否始终成立,若成立,请证明;若不成立,请说明理由.
是否始终成立,若成立,请证明;若不成立,请说明理由.
【答案】(1)详见解析;(2)成立.
【解析】
(1)由图形得∠BAE=∠BAD+45°,由外角定理,得∠CDA=∠BAD+45°,可得∠BAE=∠CDA,根据∠B=∠C=45°,证明两个三角形相似;
(2)将△ACE绕点A顺时针旋转90°至△ABH位置,证明△EAD≌△HAD转化DE、EC,使所求线段集中在Rt△BHD中利用勾股定理解决.
(1)∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°,
∴∠BAE=∠CDA,
又∠B=∠C=45°,
∴△ABE∽△DCA;
(2)成立.如图,将△ACE绕点A顺时针旋转90°至△ABH位置,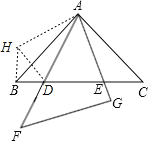
则CE=BH,AE=AH,∠ABH=∠C=45°,旋转角∠EAH=90°.
连接HD,在△EAD和△HAD中,
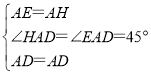
∴△EAD≌△HAD(SAS).
∴DH=DE.
又∠HBD=∠ABH+∠ABD=90°,
∴BD2+BH2=HD2,即BD2+CE2=DE2.


科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 是线段
是线段![]() 的一个三等分点,以点
的一个三等分点,以点![]() 为圆心,
为圆心,![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
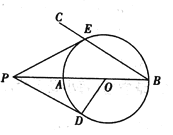
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 上的一动点,连接
上的一动点,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
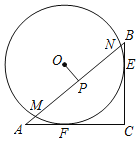
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.直径为5的⊙O分别与AC、BC相切于点F、E,与AB交于点M、N,过点O作OP⊥MN于P,则OP的长为( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
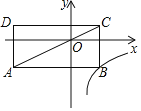
【题目】如图,在直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数y=![]() (k≠0,x>0)的图像上,点D的坐标为(-4,1),则K的值为( )
(k≠0,x>0)的图像上,点D的坐标为(-4,1),则K的值为( )
A.![]() B.
B.![]() C.4D.-4
C.4D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2)。
(1)若点(-![]() ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;
(2)若点A为抛物线顶点,且抛物线过点(1,1)。
①求抛物线的解析式;
②若点M是抛物线上异于点A的一个动点,点P与点O关于点A对称,直线MP交抛物线与另一个点N,点N’是抛物线上点N关于对称轴的对称点,直线PN’与抛物线交于点E,求证:直线EN恒过点O。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有两个相邻内角和等于另两个内角和的一半的四边形称为半四边形,这两个角的夹边称为对半线.
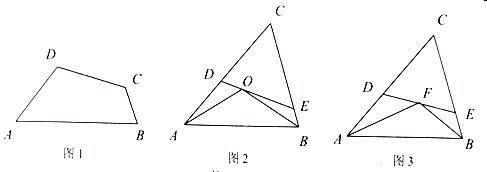
(1)如图1,在对半四边形![]() 中,
中,![]() ,求
,求![]() 与
与![]() 的度数之和;
的度数之和;
(2)如图2,![]() 为锐角
为锐角![]() 的外心,过点
的外心,过点![]() 的直线交
的直线交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是对半四边形;
是对半四边形;
(3)如图3,在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,当
,当![]() 为对半四边形
为对半四边形![]() 的对半线时,求
的对半线时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
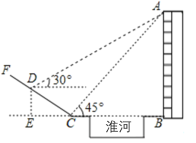
【题目】如图,在淮河的右岸边有一高楼,左岸边有一坡度![]() 的山坡
的山坡![]() ,点
,点![]() 与点
与点![]() 在同一水平面上,
在同一水平面上,![]() 与
与![]() 在同一平面内.某数学兴趣小组为了测量楼
在同一平面内.某数学兴趣小组为了测量楼![]() 的高度,在坡底
的高度,在坡底![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,然后沿坡面
,然后沿坡面![]() 上行了
上行了![]() 米到达点
米到达点![]() 处,此时在
处,此时在![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,求楼
,求楼![]() 的高度.(结果保留整数)(参考数
的高度.(结果保留整数)(参考数![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
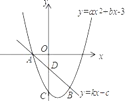
【题目】抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.
(1)求抛物线的解析式;
(2)求出C、D两点的坐标
(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com