
| A. | -20 | B. | -19 | C. | -15 | D. | -13 |
分析 解不等式组中的两个不等式,根据不等式组无解得出a的范围;解分式方程知x=$\frac{9}{a+2}$,由分式方程有整数解之知$\frac{9}{a+2}$=±1、-3、±9,求得a的值后求和即可得.
解答 解:解不等式$\frac{1}{2}$(x-3)+$\frac{x}{2}$≥3得x≥$\frac{9}{2}$,
解不等式$\frac{a-3x}{3}$>0,得:x<$\frac{a}{3}$,
∵不等式组无解,
∴$\frac{a}{3}$≤$\frac{9}{2}$,
解得a≤$\frac{27}{2}$;
解方程 $\frac{ax}{x-3}+\frac{3}{3-x}$=-2得x=$\frac{9}{a+2}$,
∵分式方程有整数解,
∴$\frac{9}{a+2}$=±1、-3、±9,
解得:a=-1或-3或-5或-11或7,
∴所有满足条件的a值的和为-1-3-5-11+7=-13,
故选:D
点评 本题主要考查解一元一次不等式组和分式方程的能力,解题的关键是熟练掌握解不等式(组)和分式方程的基本技能,并求得符合条件的a的值.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
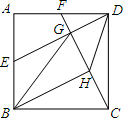 如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH.
如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,FG为⊙O的直径,$\widehat{HF}$=$\widehat{HG}$,E为$\widehat{HF}$上一点,延长FE至点A,使EA=EG,连接HG.
如图,FG为⊙O的直径,$\widehat{HF}$=$\widehat{HG}$,E为$\widehat{HF}$上一点,延长FE至点A,使EA=EG,连接HG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com