
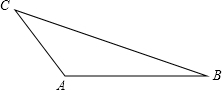
 如图,△ABC为钝角三角形(∠A>90°)
如图,△ABC为钝角三角形(∠A>90°) 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
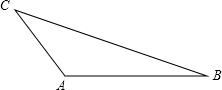 如图,△ABC为钝角三角形(∠A>90°)
如图,△ABC为钝角三角形(∠A>90°)查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
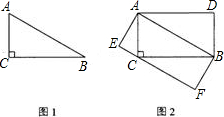
阅读下面短文:如图(1)△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对上,那么符合要求的矩形可以画出两个:矩形ACBD和矩形AEFB[如图(2)].
解答问题:
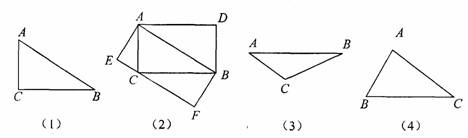
(1)设图中矩形ACBD和矩形AEFB面积分别是S1,S2,则S1 S2 (填“>”,“=”或“<”)
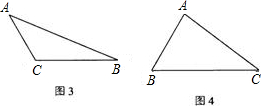
(2)如图,△ABC是钝角三角形,按短文中要求把它补成矩形,那么符合要求的矩形可以画出 个,利用图(3)把它画出来.
(3)如图(4),△ABC是锐角三角形且三边满足BC>AC>AB,按短文要求把它补成矩形,那么符合要求的矩形可以画出 个,利用图(4)把它画出来.
(4)在图(4)中画出的矩形中,哪一个周长最小?为什么?
查看答案和解析>>
科目:初中数学 来源:2002年陕西省中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com