
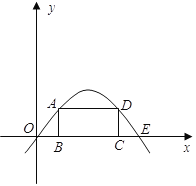
【题目】如图:矩形ABCD的顶点B、C在x轴的正半轴上,A、D在抛物线![]() 上,矩形的顶点均为动点,且矩形在抛物线与
上,矩形的顶点均为动点,且矩形在抛物线与![]() 轴围成的区域里。
轴围成的区域里。
(1)设A点的坐标为(![]() ,
, ![]() ),试求矩形周长
),试求矩形周长![]() 关于变量
关于变量![]() 的函数表达式;
的函数表达式;
(2)是否存在这样的矩形,它的周长为9,试证明你的结论。
【答案】(1)![]() (2)不存在,证明见解析.
(2)不存在,证明见解析.
【解析】试题分析:(1)根据抛物线的解析式令y=0,可求出抛物线与x轴两交点的坐标,因为A点的坐标为(x,y),则B点坐标为(x,0),即OB=x,由抛物线的对称性可知EC=x,则BC=4-2x,再根据矩形的面积公式可求出矩形周长p关于变量x的函数表达式;
(2)先假设符合条件的矩形存在,把9代入(1)所求的矩形周长公式,根据一元二次方程判别式的情况判断出方程解的情况即可判断P是否存在.
试题解析:(1)令![]() =0
=0
得:x1=0,x2=4.
则抛物线与坐标轴两交点的坐标为O(0,0)、E(4,0)
设OB=x,由抛物线的对称性可知EC=x,则BC=42x.
P=2(42x+y)=2(42x ![]() )
)
P=![]()
(2)不存在。
若存在周长为9的矩形ABCD,则![]() =9
=9
①4x24x+3=0,△=1648<0
方程①无实数根,即不存在这样的矩形。


科目:初中数学 来源: 题型:
【题目】某科学技术协会为倡导青少年主动进行研究性学习,积极研究身边的科学问题,组织了以“体验、创新、成长”为主题的青少年科技创大赛,在层层选拔的基础上,所有推荐参赛学生分别获得了一、二、三等奖和纪念奖,工作人员根据获奖情况绘制成如图所示的两幅不完整的统计图,根据图中所给出的信息解答下列问题:
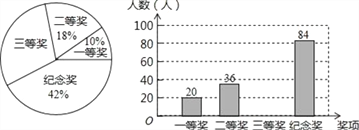
(1)这次大赛获得三等奖的学生有多少人?
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示三等奖扇形的圆心角是多少度?
(4)若给所有推荐参赛学生每人发一张相同的卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出写有一等奖学生名字卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )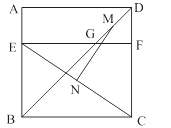
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
阅读材料:
如图,在四边形ABCD中,对角线AC⊥BD,垂足为P.
求证:S四边形ABCD=![]()
证明:AC⊥BD→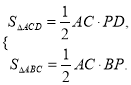
∴S四边形ABCD=S△ACD+S△ACB= ![]()
=![]()
解答问题:
(1)上述证明得到的性质可叙述为_______________________________________.
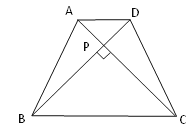
(2)已知:如图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD=3cm,BC=7cm,利用上述的性质求梯形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com