
【题目】如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为( ) 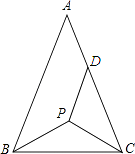
A.20°
B.30°
C.32°
D.36°
【答案】D
【解析】解:连接AP, 
∵P为其底角平分线的交点,
∴点P是△ABC的内心,
∴AP平分∠BAC,
∵AB=AC,
∴∠ABC=∠ACB,
设∠A=2x,则∠DAP=x,∠PBC=∠PCB=45°﹣ ![]() x,
x,
∵DA=DP,
∴∠DAP=∠DPA,
由折叠的性质可得:∠PDC=∠PBC=45°﹣ ![]() x,
x,
则∠ADP=180°﹣∠PDC=135°+ ![]() x,
x,
在△ADP中,∠DAP+∠DPA+∠ADP=180°,即x+x+135°+ ![]() x=180°,
x=180°,
解得:x=18,
则∠A=2x=36°.
故选D.
由题意可得点P是△ABC的内心,连接AP,则AP平分∠BAC,设∠A=2x,分别表示出∠PBC,∠PCD,在△APD中利用三角形的内角和为180°,可得出x的值,继而得出答案.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAE,DA∥CE,AB=CB. 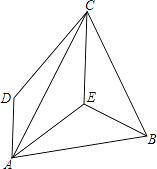
(1)试判断BE与AC有何位置关系?并证明你的结论;
(2)若∠DAC=25°,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
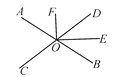
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.

(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(3x﹣1)5=a0+a1x+a2x2+…+a5x5 , 则a1+2a2x+3a3x+4a4+5a5=( )
A.80
B.120
C.180
D.240
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com