

 )
) 
 y=x-2,y=
y=x-2,y=
 =1,纵坐标为
=1,纵坐标为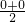 ,则E点坐标为(1,0);
,则E点坐标为(1,0);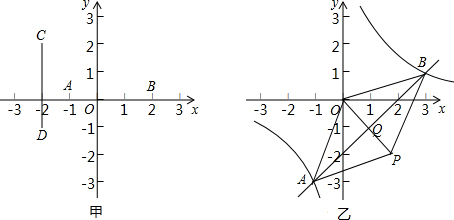
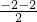 =-2,纵坐标为
=-2,纵坐标为 =
= ,则F点的坐标为(-2,
,则F点的坐标为(-2, );
); ,y=
,y= ;
;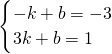 ,解得
,解得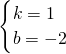 ,
,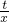 ,
, ;
; ,
,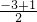 ),即Q(1,-1),
),即Q(1,-1),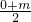 =1,
=1, =-1,解得m=2,n=-2,
=-1,解得m=2,n=-2, );
); ,
, ;y=x-2,y=
;y=x-2,y= .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.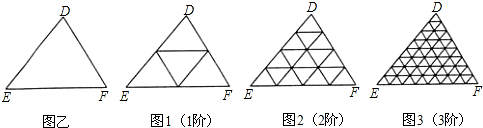
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届浙江省丽水市庆元县中考模拟数学试卷(带解析) 题型:解答题
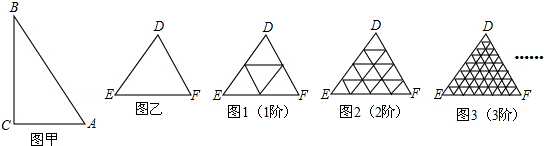
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
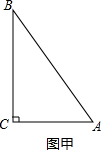
探究:(1)如图甲,已知△ABC中∠C=90°,你能把△ABC分割成2个与它自己相似的小直角三角形吗?若能,请在图甲中画出分割线,并说明理由.
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可将原三分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割,称为1阶分割(如图1);把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割,称为2阶分割(如图2)……依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形(n为正整数),设此时小三角形的面积为Sn.
①若△DEF的面积为1000,当n为何值时,3<Sn<4?
(请用计算器进行探索,要求至少写出二次的尝试估算过程)
②当n>1时,请写出一个反映Sn-1,Sn,Sn+1之间关系的等式(不必证明)

查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省丽水市庆元县中考模拟数学试卷(解析版) 题型:解答题
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
探究:(1)如图甲,已知△ABC中∠C=90°,你能把△ABC分割成2个与它自己相似的小直角三角形吗?若能,请在图甲中画出分割线,并说明理由.
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可将原三分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割,称为1阶分割(如图1);把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割,称为2阶分割(如图2)……依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形(n为正整数),设此时小三角形的面积为Sn.
①若△DEF的面积为1000,当n为何值时,3<Sn<4?
(请用计算器进行探索,要求至少写出二次的尝试估算过程)
②当n>1时,请写出一个反映Sn-1,Sn,Sn+1之间关系的等式(不必证明)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com