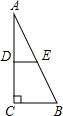有一张矩形纸片ABCD.AD=9.AB=12.将纸片折叠使A.C两点重合.那么折痕长是．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

有一张矩形纸片ABCD，AD=9，AB=12，将纸片折叠使A、C两点重合，那么折痕长是

．

分析：首先由勾股定理求出AC的长，设AC的中点为E，折线与AB交于F．然后求证△AEF∽△ABC求出EF的长．

解答：

解：如图，由勾股定理易得AC=15，设AC的中点为E，折线FG与AB交于F，（折线垂直平分对角线AC），AE=7.5．
∵∠AEF=∠B=90°，∠EAF是公共角，
∴△AEF∽△ABC，
∴

．
∴EF=

22.5

．
∴折线长=2EF=

．
故答案为

．

点评：本题综合考查了矩形的性质，勾股定理，相似，全等等知识点．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有两个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（　　）

A、1

B、2

C、3

D、4

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在一张△ABC纸片中， ∠C＝90°， ∠B＝60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有一个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为

(　　)

A．1 B．2 C．3 D．4

查看答案和解析>>

科目：初中数学 来源：2013届江苏省无锡市北塘区九年级中考二模数学试卷（带解析） 题型：解答题

如图1，已知有一张三角形纸片ABC的一边AB=10，若D为AB边上的点，过点D作DE//BC交AC于点E，分别过点D、E作DF⊥BC，EG⊥BC，垂足分别为点F、点G，把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠，点A、B、C分别落在A´、B´、C´处．若A´、B´、C´在矩形DFGE内或者其边上，且互不重合，此时我们称△A´B´C´（即图中阴影部分）为“重叠三角形”．

（1）实验操作：当AD=4时，①若∠A=90°，AB=AC，请在图2中画出“重叠三角形”，= ；
②若AB=AC，BC=12，如图3，= ；③若∠B=30°，∠C=45°，如图4，= ；
（2）实验探究：若△ABC为等边三角形（如图5），设AD的长为m，若重叠三角形A´B´C´存在，试用含m的代数式表示重叠三角形A´B´C´的面积，并写出m的取值范围．