
【题目】如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )

A. 140° B. 120° C. 130° D. 无法确定
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() (k>0)在第一象限内的图象经过点A,与BC交于点F.
(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 
(1)先求解下列两题: ①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数 ![]() 的图象经过点B,D,求k的值.
的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆货车分别从![]() 、
、![]() 两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知
两地出发,沿同一条公路相向而行,当到达对方的出发地后立即装卸货物,5分钟后再按原路以原速度返回各自的出发地,已知![]() 、
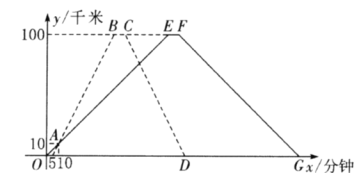
、![]() 两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程
两地相距100千米.甲车比乙车早5分钟出发,甲车出发10分钟时两车都行驶了10千米,甲、乙两车离各自出发地的路程![]() (千米)与甲车出发时间
(千米)与甲车出发时间![]() (分钟)的函数图像如图所示.
(分钟)的函数图像如图所示.
(1)甲车从![]() 地出发后,经过多长时间甲、乙两车第一次相遇?
地出发后,经过多长时间甲、乙两车第一次相遇?
(2)乙车从![]() 地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
地出发后,经过多长时间甲、乙两车与各自出发地的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
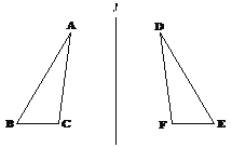
【题目】如图所示,是用笔尖扎重叠的纸得到的成轴对称的图案,请根据图形写出:
(1)两组对应点:__________和__________;
(2)两组对应线段:__________和__________;
(3)两组对应角:__________和__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.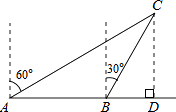
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去).
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
电量(度) | 电费(元) | |
A | 240 | |
B | ||
合计 | 90 |
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数 ![]() 经过正方形AOBC对角线的交点,半径为(4﹣2
经过正方形AOBC对角线的交点,半径为(4﹣2 ![]() )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 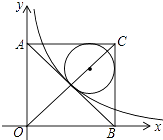
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com