
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.

解:(1)x2﹣7x+12=0,
解得x1=3,x2=4,
∵OA>OB,
∴OA=4,OB=3,
过D作DE⊥y于点E,
∵正方形ABCD,
∴AD=AB,∠DAB=90°,
∠DAE+∠OAB=90°,
∠ABO+∠OAB=90°,
∴∠ABO=∠DAE,
∵DE⊥AE,
∴∠AED=90°=∠AOB,
在△DAE和△ABO中,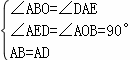 ,
,
∴△DAE≌△ABO(AAS),
∴DE=OA=4,AE=OB=3,
∴OE=7,
∴D(4,7);
(2)过点C作CM⊥x轴于点M,
同上可证得△BCM≌△ABO,
∴CM=OB=3,BM=OA=4,
∴OM=7,
∴C(7,3),
设直线BC的解析式为y=kx+b(k≠0,k、b为常数),
代入B(3,0),C(7,3)得,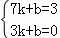 ,
,
解得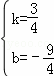 ,
,
∴y=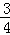 x﹣
x﹣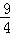 ;
;
(3)存在.
点P与点B重合时,P1(3,0),
点P与点B关于点C对称时,P2(11,6).



科目:初中数学 来源: 题型:
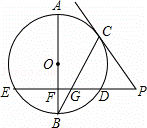
如图,已知AB是⊙O的直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C的直线与ED的延长线交于点P,PC=PG.
(1)求证:PC是⊙O的切线;
(2)当点C在劣弧AD上运动时,其他条件不变,若BG2=BF•BO.求证:点G是BC的中点;
(3)在满足(2)的条件下,AB=10,ED=4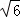 ,求BG的长.
,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
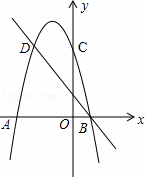
如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(二),有一圆通过四边形ABCD的三顶点A、B、D,且此圆的半径为10。若ÐA=ÐB=90°,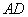 =12,
=12,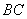 =35,则四边形ABCD的面积为何?
=35,则四边形ABCD的面积为何?
(A) 288 (B) 376 (C) 420 (D) 470
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
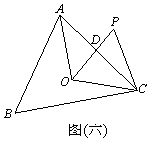
如图(六),O为△ABC的外心,△OCP为正三角形,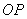 与
与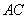 相交于D点,连接
相交于D点,连接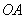 。若ÐBAC=70°,
。若ÐBAC=70°, =
=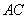 ,则ÐADP的度数为何?
,则ÐADP的度数为何?
(A) 85 (B) 90 (C) 95 (D) 110
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(十五),P为圆O外一点,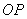 交圆O于A点,且
交圆O于A点,且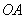 =2
=2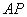 。甲、乙两人想作一条通过P点且与圆O相切的直线,其作法如下:
。甲、乙两人想作一条通过P点且与圆O相切的直线,其作法如下:
(甲) 以P为圆心,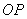 长为半径画弧,交圆O于B点,则直线PB即为所求
长为半径画弧,交圆O于B点,则直线PB即为所求
(乙) 作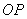 的中垂线,交圆O于B点,则直线PB即为所求对于甲、乙两人的作法,下列判断何者正确?
的中垂线,交圆O于B点,则直线PB即为所求对于甲、乙两人的作法,下列判断何者正确?
(A) 两人皆正确 (B) 两人皆错误 (C) 甲正确,乙错误 (D) 甲错误,乙正确
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2,
其中正确的结论有( )
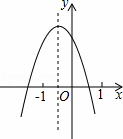
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com