
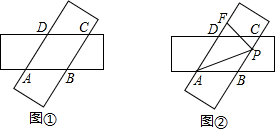
分析 (1)过点D作DE⊥AB于E,作DQ⊥BC于Q,构造全等三角形,得出AD=CD,再根据AB∥CD,AD∥BC,得到四边形ABCD是平行四边形,进而得出四边形ABCD是菱形;
(2)①先根据菱形的面积求得菱形的边长,再根据sin∠DAE的值,求得∠BAD的度数;②根据CP=4$\sqrt{2}$-2,以及∠PCG=∠BAD=45°,求得PG=4$\sqrt{2}$-2,再根据FG=PF-PG=6-4$\sqrt{2}$,以及∠CDF=45°=∠DGF,即可得到DF=FG=6-4$\sqrt{2}$.
解答 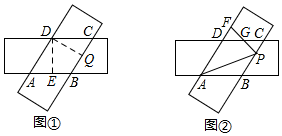 解:(1)如图1,过点D作DE⊥AB于E,作DQ⊥BC于Q,则∠AED=∠CQD=90°,
解:(1)如图1,过点D作DE⊥AB于E,作DQ⊥BC于Q,则∠AED=∠CQD=90°,
∵矩形纸片宽度均为4,
∴DE=DQ,
又∵∠CDE=∠ADQ=90°,
∴∠ADE=∠CDQ,
在△ADE和△CDQ中,
$\left\{\begin{array}{l}{∠ADE=∠CDQ}\\{DE=DQ}\\{∠AED=∠CQD}\end{array}\right.$,
∴△ADE≌△CDQ(ASA),
∴AD=CD,
又∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)①如图1,∵S四边形ABCD=16$\sqrt{2}$,
∴AB×DE=16$\sqrt{2}$,即AB×4=16$\sqrt{2}$,
∴AB=4$\sqrt{2}$=AD,
∴sin∠DAE=$\frac{DE}{AD}$=$\frac{4}{4\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴∠BAD=45°;
②如图2,∵菱形ABCD中,AB=BC=4$\sqrt{2}$,而PB=2,
∴CP=4$\sqrt{2}$-2,
又∵PF⊥AD,AD∥BC,
∴PF⊥BC,
又∵∠PCG=∠BAD=45°,
∴PG=4$\sqrt{2}$-2,
∴FG=PF-PG=4-(4$\sqrt{2}$-2)=6-4$\sqrt{2}$,
又∵∠CDF=45°=∠DGF,
∴DF=FG=6-4$\sqrt{2}$.
点评 本题主要考查了菱形的判定,全等三角形的判定与性质,矩形的性质以及解直角三角形的综合应用,解决问题的关键是作辅助线构造全等三角形.解题时注意:一组邻边相等的平行四边形是菱形.


科目:初中数学 来源: 题型:解答题
 足球比赛中,守门员根据场上攻守情况在门前来回跑动,若以球门线为基准,向前跑记作正数,返回跑记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)
足球比赛中,守门员根据场上攻守情况在门前来回跑动,若以球门线为基准,向前跑记作正数,返回跑记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
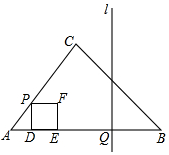 如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(s).
如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:
小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
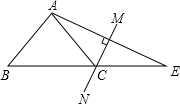 如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )| A. | 45° | B. | 48° | C. | 50° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 增减量/辆 | +3 | -2 | -1 | +4 | +2 | -5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com